Potrzebuje pomocy bo się pogubiłam w tym zadaniu
Ada: Oblicz objętość i pole powierzchni całkowitej ostrosłupa prawidłowego czworokątnego , którego
pole powierzchni bocznej wynosi 144 , a kąt nachylenia ściany bocznej do podstawy ma miarę 60
stopni
zatrzymałam się na wyznaczeniu cos 60 stopni 1/2 a przez hb zachodzi równośc hb=a
póżniej wiem ze pitagorasem mozna z notatek wyszły wartosci do podstawienia pod pitagorasa
H + 3√2 = 6√ 2
H oznacza do kwadratu
no i nie wiem skad te wartosci wlasnie 3√ 2 i 6√ 2 ktos wyjasni to zadanie , bede wdzieczna bóg
zapłać
23 kwi 20:09
Ada: Tylko nie zostawiajcie mnie samej z problemem tym bo nie zasne dzis

23 kwi 20:30
Janek191:
P
b = 4*0,5 a*h
b = 144
a h
b = 72
| | 0,5 a | |
cos α = |
| = 0,5 ⇒ 0,5a = 0,5 hb ⇒ hb = a |
| | hb | |
zatem
a
2 = 36*2
a = 6
√2
więc
| | 1 | | 3 | |
h2 =( hb)2 − (0,5 a)2 = a2 − |
| a2 = |
| a2 |
| | 4 | | 4 | |
h = 0,5
√3 a
oraz
P
c = a
2 + P
b = 72 + 144 = 216 j
2
| | 1 | | 1 | |
V = |
| a2 *h = |
| *72* 0,5 √3*6√2 = ... |
| | 3 | | 3 | |
23 kwi 20:31
Ada: dziekuje
23 kwi 20:38
Janek191:
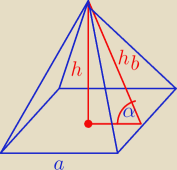
23 kwi 20:41
Mila:
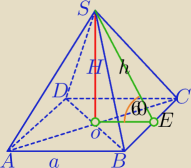
| | 1 | | 1 | |
1) |OE|= |
| a, h=2* |
| a=a ( ΔSOE: 90,60,30 ) |
| | 2 | | 2 | |
2)
2*a*a=144
a
2=72⇔a=
√72=
√36*2=6
√2
a=6√2
Jeśli chcesz H obliczyć z tw. Pitagorasa to tak:
| | 1 | | 1 | |
W ΔSOE: |OE|= |
| *a= |
| *6√2=3√2, h=6√2 |
| | 2 | | 2 | |
H
2+(3
√2)
2=(6
√2)
2
H
2=36*2−9*2
H
2=54⇔H=
√54=
√9*6
H=3
√6
3)
V=36
√6 [j
3]
=======
23 kwi 20:48


