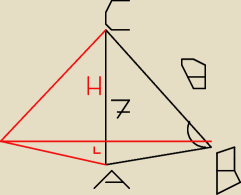
 W trójkącie ABC AC= 7 BC =8 zaś kąt ABC = 60 stopni Oblicz objętosc bryły powstałej z obrotu
trójkąta ABC wokoł prostej zawierającej bok AC.
Wyliczam z twierdzenia cosinusow bok AB i wychodzą dwa warianty 3 oraz 5. Obydwa przyjmuję. I
teraz obliczam pole ABC dla tych roznych boków. Pierwszy wynik się zgadza lecz dla boku 3
wychodza jakies glupoty.
Mianowicie Pole ABC wynosi 6√3 Teraz przyrownuje to jako pole i licze promień. Promień
wychodzi 12√3/7.
i teraz jak sobie zrobie z pitagorasa by wyliczyc H to H wychodzi 52/7 a jest to wiecej niż 7,
a musi byc rowne ten odcniek CA. Dlaczego tak sie dzieje co robię zle ? Moglby ktos to
rozwiazac bede mega wdzieczny ?
W trójkącie ABC AC= 7 BC =8 zaś kąt ABC = 60 stopni Oblicz objętosc bryły powstałej z obrotu
trójkąta ABC wokoł prostej zawierającej bok AC.
Wyliczam z twierdzenia cosinusow bok AB i wychodzą dwa warianty 3 oraz 5. Obydwa przyjmuję. I
teraz obliczam pole ABC dla tych roznych boków. Pierwszy wynik się zgadza lecz dla boku 3
wychodza jakies glupoty.
Mianowicie Pole ABC wynosi 6√3 Teraz przyrownuje to jako pole i licze promień. Promień
wychodzi 12√3/7.
i teraz jak sobie zrobie z pitagorasa by wyliczyc H to H wychodzi 52/7 a jest to wiecej niż 7,
a musi byc rowne ten odcniek CA. Dlaczego tak sie dzieje co robię zle ? Moglby ktos to
rozwiazac bede mega wdzieczny ?
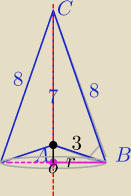 Jeżeli masz trójkąt o bokach 8,3 , 7 to kąt leżący naprzeciw boku 8 jest rozwarty.
α≈98o.
Dalej sam policzysz? Czy trzeba pomagać, bo widzę, że dobrze się orientujesz.
Jeżeli masz trójkąt o bokach 8,3 , 7 to kąt leżący naprzeciw boku 8 jest rozwarty.
α≈98o.
Dalej sam policzysz? Czy trzeba pomagać, bo widzę, że dobrze się orientujesz.


| 1 | ||
1) PΔABC= | *3*8*sin69o=6√3 | |
| 2 |
| 1 | ||
PΔABC= | *7*r=6√3 | |
| 2 |
| 12√3 | ||
r= | − promień podstawy stożka B'BC i stożka B'BA | |
| 7 |
| 1 | ||
Vbryły= | (π*r2*|OC|−πr2*|OA|}= | |
| 3 |
| 1 | 1 | |||
= | π*r2*(|OC|−|OA|)= | π*r2*|AC| | ||
| 3 | 3 |
| 1 | 12√3 | |||
V= | *( | π)2*7 | ||
| 3 | 7 |
| 1 | 144*3π | |||
V= | * | *7 | ||
| 3 | 49 |
| 144π | ||
V= | [j3] | |
| 7 |