Monotoniczność funkcji f(x) = x^3 -x w przedziale (1,+∞) XczyY: f(x) = x³ −x Mam sprawdzić czy funkcja jest rosnąca w przedziale (1,+∞) Czy jestem to w stanie zrobić na podstawie pochodnej tej funkcji? Pochodną jest funkcja kwadratowa, czy na podstawie wierzchołka pochodnej jestem w stanie stwierdzić jak zachowa się ta funkcja w danym przedziale?

aniabb: nie tyle wierzchołka co miejsc zerowych

XczyY: f'(x)=3x²−1 x1 = √3/3 x2= −√3/3 Max wartość przyjmuje dla −√3/3 Tak? W jaki sposób mogę odczytywać z wykresu pochodnej monotoniczność f(x)?

XczyY: O co ja zapytałem... brak słów x1 [P{3}/3]<1 na tej podstawie mogę stwierdzić, że funkcja jest rosnąca w przedziale (1,+∞) tak?

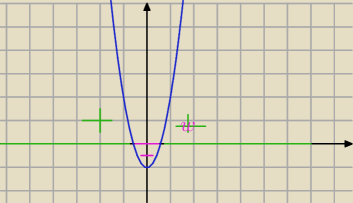
aniabb: dla zielonych x rośnie, dla różowych x maleje

XczyY: Bardzo dziękuje