Geometria analityczna - trapez równoramienny, promień
Gustavo: Pary liczb (x,y) spełniające układ równań
−4x2+y2+2y+1=0
−x2+y+4=0
Wyznacz równanie okręgu opisanego na czworokąćie ABCD.
Wychodzi trapez równoramienny z tych punktów, punkty to (−1, −3), (1, −3), (3,5), (−3,5), tak
żeby oszczędzić liczenia.
Muszę robić jakis błąd, ale chyba obliczenia się zgadzają, a wychodzi inny promień.
22 kwi 21:33
aniabb:
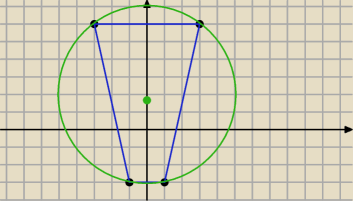
22 kwi 21:48
aniabb: a=0 b=3/2 r=√85/2
22 kwi 21:51
Gustavo: To znaczy tyle to wiem, bo mam taką odpowiedź w książce. Ale jak to obliczyć? Nie chcę robić
zadań z analitycznej, rysując na wykresie stricte.
23 kwi 13:23
aniabb: układ 4 równań z 3 niewiadomymi ... jak robisz błąd to wpisz je .. znajdziemy
23 kwi 13:28
Gustavo: Tzn ja to postanowiłem zrobić metodą taką, że przedłużyłem jeden z boków trapezu, połączyłem z
wysokoscią i wyszedł trójkąt prostokątny z wysokoscią, przedłużonym bokiem oraz przekątną.
Obliczyłem sinus kąta przy boku oraz przekątnej i z tego policzyłem pole trójkąta ze wzoru
1/2*a*b*sina. Potem obliczyłem z tego promień okręgu opisanego na tym trójkącie ze wzoru
R=abc/4P i uznałem, że to ten sam promień, co dla tegoż trapezu.
I rzeczywiscie wyszedł mi sinus sqrt(80)/1−, P=4sqrt(85)/5, potem jak patrzę w notatkach to R
mi wyszło sqrt(85)/2. Tylko nie wiem, jak obliczyć ten punkt 3/2.
23 kwi 14:06
Gustavo: A nie, przepraszam, R mi wyszło 5. xD
23 kwi 14:08
aniabb: nadal jako odległość między punktami co sprowadza się do tego samego układu 4 równań

(−1−a)
2+(−3−b)
2 = r
2
(1−a)
2+(−3−b)
2 = r
2
(−3−a)
2+(5−b)
2 = r
2
(3−a)
2+(5−b)
2 = r
2
23 kwi 14:19
Mila:
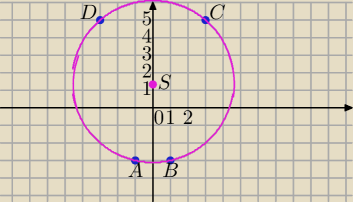
Współrzędne wierzchołków czworokąta:
A(−1, −3), B(1, −3), C(3,5),D (−3,5)
1) symetralna AB:
2) symetralna BC:
P(x,y)∊symetralnej⇔
(x+1)
2+(y+3)
2=(x−3)
2+(y−5)
2⇔
3) punkt przecięcia symetralnych:
4)Promień okręgu:
| | 3 | |
r=|SA|=√(−1−0)2+(−3− |
| )2=√1+4.52=√21.25 |
| | 2 | |
4)
23 kwi 18:23
Gustavo: Ok, dzięki.
24 kwi 14:32

 (−1−a)2+(−3−b)2 = r2
(1−a)2+(−3−b)2 = r2
(−3−a)2+(5−b)2 = r2
(3−a)2+(5−b)2 = r2
(−1−a)2+(−3−b)2 = r2
(1−a)2+(−3−b)2 = r2
(−3−a)2+(5−b)2 = r2
(3−a)2+(5−b)2 = r2
 Współrzędne wierzchołków czworokąta:
A(−1, −3), B(1, −3), C(3,5),D (−3,5)
1) symetralna AB:
Współrzędne wierzchołków czworokąta:
A(−1, −3), B(1, −3), C(3,5),D (−3,5)
1) symetralna AB: