Asymptoty Kamil: Jak znaleźć wszystkie asymptoty następującej funkcji f(x)= (x2−4)/(x2+x−2). Bardzo proszę o pomoc

Kamil: (x²−4)/(x²+x−2) poprawka

Bogdan:

	x2 − 4
a nie lepiej tak f(x) =		?
	x2 + x − 2

Bogdan:

	(x − 2)(x + 2)
a jeszcze lepiej tak: f(x) =		= ... ? bo to trudne?
	(x − 1)(x + 2)

Kamil: Hmm w pytaniu o coś innego chodziło

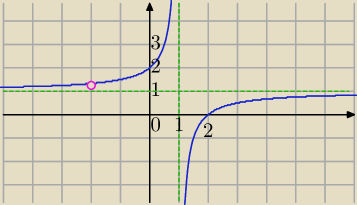
aniabb: o to ze tak zobaczysz asymptoty x=1 i y=1

Kamil: Gdy granica przy x−> −2 z lewej inz prawej strony wynosi 3/4 to dla tej granicy jaka jest asymptota?

aniabb: dla tej nie ma bo widać że się skraca z górą dlatego mówię że z tej postaci widać dlatego zostaje tylko pionowa x=1 i widać że pozioma y=1

Kamil: Przypadkiem tutaj nie ma asymptoty pionowej ? Jak to sprawdzić

aniabb: tutaj czyli gdzie?

Kamil: y=1 jest asymptotą poziomą w obu nieskończonościach . Czyli brak ukośnej

aniabb: tak

Kamil: Jak obliczyć asymptotę pionową ?

Kamil: Jak obliczyć asymptotę pionową ?

aniabb: licząc granicę w x→1

Kamil: to dla granicy −2⁻ i −2⁺ mogę napisać , że asymptota nie istnieje ?

aniabb: tak

Kamil: Czyli dla x=−2 asymptota nie istnieje ?

aniabb: tak

Mila:

	x2−4
f(x)=
	x2+x−2

	(x−2)*(x+2)
f(x)=
	(x−1)*(x+2)

D=R\{1,−2}

	x−2		x−1−1
f(x)=		=
	x−1		x−1

	−1
f(x)=1+		to znana funkcja dla Ciebie?
	x−1

Asymptoty poziome : y=1 asymptota pionowa x=1 Jeśli nie pamiętasz własności f. homograficznej to liczysz granice lim _x→±∞f(x)=1 asymptota pozioma

	−1
limx→1+ (1+		)=−∞
	x−1

	−1
limx→1− (1+		)=∞
	x−1

Kamil: Czyli dla x=1 jest asymptota pionowa obustronna ?

aniabb: tak

kulka: mam pytanie: czy dobrze rozumiem, że można liczyć granice obustronne WYMIENNIE z własnościami funkcji homograficznej? pytam, bo spotkałam się z dwoma sposobami naraz...

annabb: Świadomość jak wygląda funkcja ułatwia liczenie granic i przewidywanie wyników