GEOMETRIA bluee: a) Udowodnij, że prosta l: 3x + 4y – 19 = 0 jest styczna do okręgów o₁ i o₂, gdzie o₁: (x – 2)² + (y – 2)² = 1 oraz o₂: (x – 6)² + (y – 4)² = 9. b) Obie proste y = 1 i x = 3 są styczne do obu okręgów. Naszkicuj rysunek okręgów o₁ i o₂, prostej l, prostej y = 1 i prostej x = 3 w układzie współrzędnych.Znajdź równanie czwartej prostej stycznej do okręgów o1 i o2. Narysuj ją. Rysunek mam już zrobiony.

	3		19
W punkcie pierwszym, podstawiłam y=−		x+		i dla o1 wyszło mi 25x2−2x+196=0
	4		4

Wiem, że to zadanie już było tu dodane https://matematykaszkolna.pl/forum/292094.html.

PW:

	3		19
(x−2)2+(−		x+		−2)2=1
	4		4

	11		3
(x−2)2+(		−		x)2=1
	4		4

	121		11	3		9
x2−4x+4+		−2			x+		x2=1
	16		4	4		16

25x²−130x+169=0 Δ=0 − równanie ma jedno rozwiązanie − prosta jest styczna do okręgu. Chyba łatiej rachunkowo byłoby użyć wzoru na odległość środka okręgu od prostej − pokazać, że odległość jest równa promieniowi okręgu.

bluee: Ze wzoru na odległość punktu od prostej dla podpunktu b). wychodzi mi 3|2A+2B+B|=|6A+4B+C| Jak to ugryź?

Jerzy: Poprawnie zastosować wzór na odległość punktu od prostej: Masz prostą: 0*x + 1*y − 1 = 0 i punkt: S(6,4)

	|0*6 + 1*4 − 1|
d =		= 3
	√02 + 12

bluee: Ale co ta prosta ma do szukanej prostej? 3|2A+2B+B|=|6A+4B+C| Powinno być 3|2A+2B+C|=|6A+4B+C| ale to tylko literówka. Metodą podstawiana wyszło mi, że y=−2x+9, ale szukana prosta musi mieć współczynnik kierunkowy a>0, więc coś jest nie tak.

aniabb: ona próbuje policzyć tę 4 prostą załóż że B=1 czyli postać jakby kierunkową wyznacz A od C i wstaw znów do wzoru na odległość

aniabb: usuwając moduły rozpatrz 2 przypadki

bluee: Dzięki za wskazówkę

bluee: 3(2A+2+C)=6A+4+C i −3(2A+2+C)=6A+4+C Tak dla pewności to są te dwa przypadki ?

aniabb: tak

bluee: Dla tego pierwszego przypadku wychodzi C=−1?

aniabb: o jak ładnie

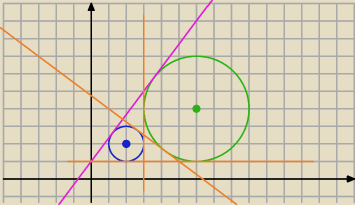
aniabb: i wtedy y=4x/3+1 (ta różowa)

bluee:

	4
A=		A co dla drugiego przypadku?
	3

bluee: No masz ja na chwilkę odeszłam od ekranu, a Ty odwaliłaś za mnie całą robotę !

aniabb: pewnie wyjdzie ta pomarańczowa z przypadku a) sprawdź

bluee:

	10+4C
W tym drugim przepadku mi wyszło −12A−4C=10, czyli powinnam podstawić A=		I
	−12

wyjdzie mi coś sprzecznego...

bluee: No tak, zapomniałam o tej pomarańczowej ...

aniabb: wyjdzie Ci ten z a) bo pasuje

bluee: Coś mi się jednak nie zgadza mi wyszło c=−1, a ty masz c=1.

bluee:

bluee: Niestety dalej nie pasuje mi to zadanie Mówimy o b). Wyszłam ze wzoru na odległość punktu od prostej i uzyskałam takie coś: 3|2A+2B+C|=|6A+4B+C| Przechodzę z postaci ogólnej do kierunkowej czyli B=0. Rozważam dwa przypadki I. 3(2A+2B+C)=6A+4B+C II. −3(2A+2B+C)=6A+4B+C

	4
Dla I. wyszło mi C=−1 i A=−		. Żeby prosta spełniała warunek styczność musi A>0.
	3

Czyli nic się nie zgadza. O II. przypadku nawet nie mówię...

aniabb: Ax+y+C=0 to jest y=−Ax−C taka drobna różnica pomiędzy kierunkową i ogólna