La gringa:
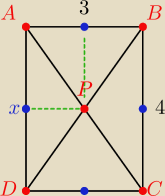
Czerwone punkty (jest ich 5) są oddalone od siebie o odległość większą niż
√2 ≈ 2,236.
Są one umiejscowione najdalej od siebie jak się da.
Pozostaje nam dać gdzieś w ten prostokąt ostatni (niebieski) punkt.
Musimy tak go umiejscowić by był on możliwie jak najdalej od pozostałych.
Najdalej będzie na środku jakiegoś boku tego prostokąta (wtedy będzie zachowana równa odległość
od innych punktów umiejscowionych na wierzchołkach i jednocześnie najdalej od środka
prostokąta.
Ponieważ odległość ostatniego punktu (punktu x) od punktów umiejscowionych na wierzchołkach
może
być równa maksymalnie 2 lub 1.5 a od punktu P maksymalnie również 1.5 lub 2, a obie te liczby
są mniejsze od
√5
Co oznacza, że zawsze będzie przynajmniej jeden punkt który będzie od innego w odległości
mniejszej od
√5
