Pomocy Kolezanki i Koledzy Anka: W ostrosłupie prawidłowym czworokątnym o krawędzi podstawy 12cm , kąt płaski sciany bocznej przy wierzchołku ostrosłupa wynosi 120 stopni . Oblicz PC i V prosze o pomoc bo kompletnie nie wiem jak zabrac sie za obliczenie wysokosci w tym zadaniu itp , jest tu jakas mocna głowa ?

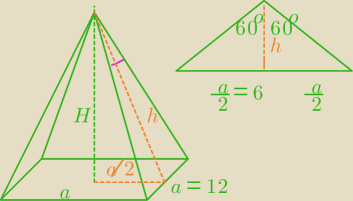
iteRacj@: na rysunku osobno jest dorysowana ściana boczna ostrosłupa

	a   2
tg 60o=
	h

z tego wylicz wysokość ściany bocznej h

	a
z tw.Pitagorasa h2=H2+(		)2
	2

oblicz H z tego równania pozostaje tylko podstawić do wzorów na PC i V

Anka: dziekuje CI juz wiem , spokojnej niedzieli człowieku dobry

iteRacj@: akurat nie jestem zbyt dobrym człowiekiem z mocną głową, ale dziękuję

Anka: wazne ze checi są a i wiedza w głowie obecna ! musze ogarnac te tematy bo zaliczenia na 5 , mam nadzieje ze mi sie uda duzo sie rozjasniło dzieki !

iteRacj@: powodzenia!

Anka: iteRacja a mam pytanie od kąta 60 stopni liczac h to nie czasem sinus ? przyprostokatna dalej polozona do przeciw prostokatnej ktora tworzy h bo tanges to by wychodzil do H ostroslupa ? i rozumiem ze 120stopni ta przekatna sciany bocznej rozbija na 2x po 60 ?

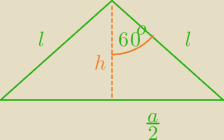
iteRacj@: Jako l oznaczyłam krawędź boczną ostrosłupa czyli ramię trójkąta tworzącego ścianę boczną. Ściana boczna ostrosłupa jest trójkątem równoramiennym. Dlatego wysokość ściany bocznej h podzieliła kąt 120^o na dwa równe kąty − czyli kąty po 60^o. I teraz zajmujemy się tylko jednym z dwóch przystających trójkątów prostokątnych utworzonych

	a
przez h, l i		. Dlaczego? Żeby można było skorzystać z tw.Pitagorasa.
	2

	a   2
tg 60o=
	h

	a   2
sin 60o=
	l

iteRacj@: Na końcu zapisałam funkcję sinus 60^o, o którą pytasz, żeby było widać, że h tam nie występuje. Więc przy tych obliczeniach nie ma potrzeby z niej korzystać.

emeryt 75: l=4√3, h jest połową l,czyli wynosi 2√3,lecz w trójkącie prostokątnym o przyprostokątnych H i a/2, h jest przeciwprostokątną i widać sprzeczność,bo 2√3 < 6,czyli przeciwprostokątna jest mniejsza od jednej z przyprostokątnych. Albo,więc jest błąd w treści zadania,albo mam sklerozę ?

iteRacj@: błąd to najprędzej jest w moim liczeniu , zaraz to sprawdzę

iteRacj@: @emeryt 75 z moich obliczeń też wynika, że nie da się przy tych danych zbudować ostrosłupa. Kąt nazwany tutaj kątem płaskim ściany bocznej przy wierzchołku ostrosłupa musi być <90^o. Dobrze, że to zauważyłeś. I jako jedyny policzyłeś zadanie do końca.

emeryt 75: Taki ostrosłup istnieje,gdy podstawą jest prostokąt,lecz nie jest to wtedy ostrosłup prawidłowy czworokątny. Pozdrawiam.