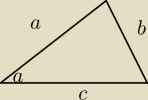
Oblicz d: Oblicz jaka może być najmniejsza możliwa dlugosc boku BC trojkata ABC,jezeli ∡BAC=α i pole ΔABC jest rowne S. Czyli: acsinα=2S

	2S
ac=
	sinα

b²=a²+c²−2accosα

	4Scosα
b2=a2+c2−		=a2+c2−4Sctgα
	sinα

co dalej?

jc: Amożetakkilkaspacji?

d: nie wiem czy spacja jest potrzebna w poprawnym rozwiazaniu

hubi:

	4S
b2=(a−c)2 +		−4Sctgα
	sinα

	4S
no i teraz nie jestem pewien ale wyrażenie		−4Sctgα wygląda mi na stałą
	sinα

więc b² będzie minimalne gdy (a−c)²=0 czyli a=c ale nie wiem czy to jest poprawne bardzo możliwe że popisałem głupoty