Zadanie optymalizacyjne .: Rozpatrujemy wszystkie trójkąty o obwodzie L i jednym z kątów o mierze 120°. Oblicz długości boków tego trójkąta, dla którego pole koła wpisanego w ten trójkąt będzie największe

La gringa: Podbijam

.: Podbijam

.: Podbijam ponownie

koza: Zastosuj tworzenie cosinusow

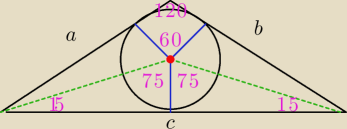
La gringa: L=a+b+c a>0; b>0; c>0; Z rysunku widać że mamy do czynienia z trójkątem równoramiennym zatem: a=b L= 2a + c Szukamy P_k max = πr²

	a+b+c		L
Promień koła wpisanego w trójkąt: r=		czyli r=
	2		2

c²=a²+a²−2*a*a*cos(120) c²=2a² − 2*a²*(cos(90+30))

	1		1
cos(90+30) = cos(90)*cos(30)−sin(90)*sin(30) = 0*U{√3{2} − 1*−		=−
	2		2

c²=2a²+a² c²=3a² /√ c₁=a√3 lub c₂=−a√3 c₂ nie spełnia założeń.

	L
L=2a+a√3 ⇔ a=
	2√3+3

[n[I dalej nie wiem jak ugryźć, przy próbie podstawienia do wyprowadzonego wzoru na pole koła czyli: ]]

	L2		2a+a√3)2
P=π		⇒P=		otrzymuję funkcję, liczę jej pochodną ale gdy liczę warunek
	22		4

konieczny do istnienia ekstremum otrzymuję a ujemne co jest sprzeczne z założeniami.

maturka: a skąd masz taki wzór na promień okregu wpisanego?

aniabb: z tablic maturalnych

maturka: a mozesz podac link gdzie taki wzór jest?

aniabb: http://prntscr.com/j8q8ob

maturka: no w linku jest inny wzór ( i do tego dla trójkata prostokatnego) niż w zadaniu i dlatego sie o to pytam

aniabb: no rzeczywiście trochę za dużo uogólnień i tu jak już to chyba powinien być wzór że P_Δ=pr

maturka: To jest powód dlaczego potem wychodzi ujemne ekstremum

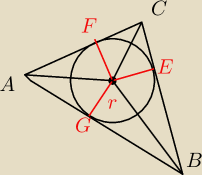
an: Skoro z góry zakładasz a=b to przy określonym l i kącie r jest określone, można przypuszczać, że a=b, ale to dopiero się okaże po obliczeniy max i boków skąd ten wzór na r powierzchnia koła będzia najwię przy r=r_max CB=x

	2r
CF=CE=r/√3 l=2x+2AC−		⇒ AC=
	√3

	lr		x*AC*sin120o
S=		=
	2		2

	√3(l/2x−x2)
r=
	2l−x

r'=.....=0 x²−4lx+l²=0 x₁=(2−√3)l x₂=(2+√3)l odrzucam x musi być mniejsze od l masz bok x policz pozostałe

lub: Czemu zakładacie ze on jest równorammienny. Wg mnie wykazanie ze on musi byc równoramienny to jest najwazniejsze.