Geometria analityczna. piotrovvicz: Dany jest trapez o wierzchołkach: A(–2; 1), B(3; –4), C(2; 3) i D(1; 4). a) Wyznacz równania prostych zawierających boki: AB, CD i AD. b) Uzasadnij, że trapez ten jest prostokątny i wyznacz jego pole.

piotrovvicz:

	3
Mam problem z równaniem prostej AB. Wyszło mi: y = –		x – 1, a w odpowiedziach jest:
	5

y = –x – 1. Czy mogę prosić o pomoc w tym zadaniu?

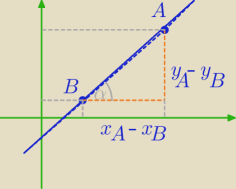
iteRacj@: współczynnik kierunkowy prostej przechodzącej przez pkty A i B mozna policzyć ze wzoru

	yA−yB		−5
aAB=		=		=−1
	xA−xB		−5

iteRacj@: rysunek jest poglądowy oczywiście

	5
i poprawka minusa		=−1
	−5

piotrovvicz: Ahhh, dobra. Miałem błąd w wyliczeniach A czy mógłbym poprosić o rozwiązanie podpunktu b)?

iteRacj@: Jakie masz współczynnki kierunkowe prostych z podpunktu a/ ?

piotrovvicz: CD: a = –1, AB: a = – 1, AD: a = 1.

iteRacj@: Czworokąt będzie trapezem, jeśli dwa jego boki (przynajmniej) będą się zawierać w prostych równoległych. Muszą to być boki przeciwległe. Trapez bedzie prostokątny, jeśli dwa jego boki (przynajmniej) będą się zawierać w prostych prostopadłych. Oczywiscie będą to boki mające wspólny wierzchołek. Sprawdź, czy podane współczynniki kierunkowe spełniają warunki prostpadłości i równoległości prostych.

piotrovvicz: |AB| jest równoległa do |CD|, bo –1 = –1 |AB| jest prostopadła do |AD|, bo (–1) · 1 = –1 |CD| jest prostopadła do |AD|, bo (–1) · 1 = –1 Czy o to chodziło?

iteRacj@: dobrze, tylko popraw zapis ale błąd w zapisie: |AB| − odległość między punktami A i B (liczba) tu chodzi o prostą AB (zbiór punktów) AB ∥ CD AB⊥AD, CD⊥ AD

piotrovvicz: Spoko. Rozumiemz że to jest te udowodnienie trapezu prostokątnego?

iteRacj@: W ten sposób uzasadnisz, że trapez jest prostokątny. Trzeba napisać, że AB ∥ CD więc czworokąt jest trapezem, oraz AB⊥AD stąd trapez jest prostokątny.

piotrovvicz: Mam tak napisane. Dziękuję za pomoc