stereometria
Natss: Przez przekatna dolnej podstawy prostopadloscianu i jeden z jego gornych wierzcholkow
poprowadzono plaszczyzne.Przekroj jest trojkatem o dwoch bokach dlugosci 2 i 3 oraz kacie
miedzy nimi rownym 60 stopni. Oblicz objetosc prostopadloscianu oraz sinus kata nachylenia
plaszczyzny podstawy
22 kwi 00:05
Basia:
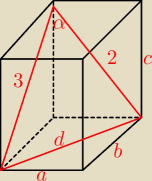
d
2 = 2
2+3
2−2*2*3*cos(60)
| | 1 | |
d2 = 4+9 − 12* |
| = 13−6 = 7 |
| | 2 | |
d =
√7
a
2+b
2 = 7
a
2+c
2 = 4
b
2+c
2 = 9
a
2+b
2 = 7
a
2−b
2 = −5 (drugie−trzecie stronami)
−−−−−−−−−−−−−−−−−−−−−−−−−−−
2a
2 = 2
a
2 = 1
a=1
b
2=6
[C[b=
√6]
c
2=3
c=√3
V = a*b*c = 1*
√6*
√3 =
√18 = 3
√2
22 kwi 00:17
Basia: z kątem nachylenia do płaszczyzny podstawy będzie trochę trudniej
spodek wysokości tego trójkąta nie jest środkiem d
wysokość nie jest też dwusieczną kąta α
muszę chwilę pomyśleć
22 kwi 00:22
Basia: Napisałeś:
Oblicz objetosc prostopadloscianu oraz sinus kata nachylenia plaszczyzny podstawy
Rozumiem, że chodzi o sinus kąta nachylenia tego trójkąta do płaszczyzny podstawy.
22 kwi 00:32
Basia:
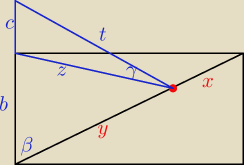
x,y − odcinki na które wysokość dzieli d
wtedy
x
2+h
2 = 2
2
y
2+h
2 = 3
2
| | √3 | |
2*Ptr = 2*3*sin(60) = 2*3* |
| = 3√3 |
| | 2 | |
2*P
tr = d*h = h
√7
stąd
h
√7 = 3
√3
z
2 = b
2+y
2−2by*cosβ
policz to bo mnie już brakuje czasu, a w ogóle nie jestem pewna czy się gdzieś nie pomyliłam
trzeba to posprawdzać
t
2 = c
2+z
2
22 kwi 00:56
Basia: to nie ten kąt; sorry
22 kwi 00:59
Basia:
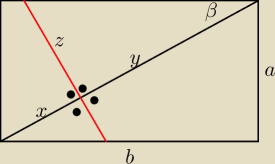
a jednak ten; tyle, że to trzeba udowodnić, bo nie zawsze tak musi być
no to jeszcze raz:
mamy policzone d=
√7; a=1; b=
√6; c=
√3
2*P
tr = 2*3*sin(60) = 3
√3
2*P
tr =
√7*h
√7*h = 3
√3
x, y − odcinki na które spodek h dzieli d
| | 6 | | 36 | | 42 | |
z2+y2 = |
| + |
| = |
| = 6 = b2 |
| | 7 | | 7 | | 7 | |
z tego wynika, że prostopadła do d przechodzi przez wierchołek podstawy
czyli szukany kąt γ jest w trójkącie prostokątnym o bokach z, c i przeciwprostokatnej h
22 kwi 01:45
Natalia : Dziekuje bardzo
22 kwi 10:50