Pole trójkąta, równanie okręgu hexx: 1. Oblicz Pole trójkąta o wierzchołkach A, B, C: A(−2,−1) B(1,3) C(−3,6) 2. Napisz równanie okręgu o promieniu √5 , jeśli punkty A i B należą do tego okręgu. A(0,4) B(−1,1) 3. Wyznacz równanie okręgu opisanego na trójkącie ABC. A(4,7) B(2,7) C(−2,5)

bezendu: https://matematykaszkolna.pl/strona/503.html

Janek191: Inny sposób : → AB = [ 3, 4 ] → AC = [ −1, 7 ] więc → → P = 0,5 I det ( AB, AC ) I = 0,5 * I 3*7 − 4*(−1) I = 0,5 * I 21 + 4 I = 0,5*25 = 12,5

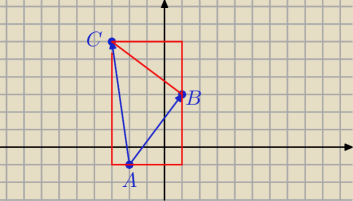
Janek191: Inny sposób: P = 4*7 − 0,5*3*4 − 0,5*1*7 − 0,5*1*4*3 = 28 − 6 − 3,5 − 6 = 12,5

hexx: A dał by radę ktoś pomóc z dwoma pozostałymi?

Janek191: z.2 ( x − a)² + ( y − b)² = r² = 5 ( 0 − a)² + ( 4 − y)² = 5 (− 1 − a)² + (1 − b)² = 5 −−−−−−−−−−−− Rozwiąż ten układ równań

Janek191: z.3 jak z. 2 ale układ trzech równań bo nie ma r.