Geometria analityczna. piotrovvicz: 1. Punkty A(–2; –9) i C(–7; 4) są końcami przekątnej kwadratu ABCD. Oblicz promień okręgu wpisanego w ten kwadrat. 2. Punkt A leży na osi OX, a punkt B ma współrzędne (–5; –4). Środek odcinka AB leży na prostej y = 2x. Oblicz długość tego odcinka.

Janek191: 1) I AC I² = ( − 7 + 2)² + ( 4 − (−9))² = 25 + 13² = 194

	194
a = I A B I = I AC I : √2 =		= 97 √2
	√2

r = 0,5 a = 48,5 √2 ===================

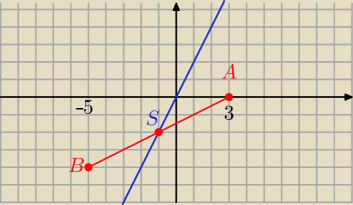
Janek191: B = ( − 5, − 4) A = ( x, 0 )

	x − 5		x − 5
S = (		, 2*		) = ( 0,5 x − 2,5 ; x − 5)
	2		2

→ → BS = SA [ 0,5 x + 2,5 , x − 1 ] = [ 0,5 x +2,5 , − x + 5 ] więc x − 1 = − x + 5 2 x = 6 x = 3 zatem A = ( 3, 0) =============== Dokończ

Janek191: Krócej : B = ( − 5, − 4) A = (x , 0) więc S = ( 0,5 ( x − 5), − 2) oraz − 2 = f( 0,5 ( x − 5)) = x − 5 ⇒ x = 3 A = ( 3, 0) ==========

piotrovvicz: Dlaczego we wzorze na środek , "y" jest pomnożone przez 2?

Janek191: x jest pomnożone przez 2, bo y = 2 x