 ...
...
 Mam jeszcze takie zadanie:
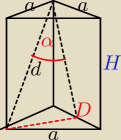
Przekątna ściany bocznej graniastosłupa prawidłowego trójkątnego ABCA`B`C` ma długość d, a
krawędź podstawy ma długość a. Wyznacz objętość graniastosłupa oraz cosinus kąta AC`D, gdzie D
jest środkiem krawędzi BC.
nie jestem pewny czy rysunek jest dobrze wykonany....
no i teraz nie wiem....
obliczyć objętość :
Mam jeszcze takie zadanie:
Przekątna ściany bocznej graniastosłupa prawidłowego trójkątnego ABCA`B`C` ma długość d, a
krawędź podstawy ma długość a. Wyznacz objętość graniastosłupa oraz cosinus kąta AC`D, gdzie D
jest środkiem krawędzi BC.
nie jestem pewny czy rysunek jest dobrze wykonany....
no i teraz nie wiem....
obliczyć objętość :
| a2√3 | ||
V = | * H | |
| 4 |
| a2√3 | ||
V = | * (d− a) ? | |
| 4 |

 Do tego zadania jest jeszcze jeden podpunkt b) wyznacz wszystkie wartości parametru m, dla
których do wykresu funkcji należy punkt A(1,1)
nie do konca wiem jak sie za to zabrać.... czy współrzędne punktu A mam podstawić do wzoru z
parametrem "m" ? i czy w czasie obliczania, również muszę rozpatrzeć dwa przypadki kiedy |m|
jest dodatnia lub ujemna?
Do tego zadania jest jeszcze jeden podpunkt b) wyznacz wszystkie wartości parametru m, dla
których do wykresu funkcji należy punkt A(1,1)
nie do konca wiem jak sie za to zabrać.... czy współrzędne punktu A mam podstawić do wzoru z
parametrem "m" ? i czy w czasie obliczania, również muszę rozpatrzeć dwa przypadki kiedy |m|
jest dodatnia lub ujemna?
 od kiedy to
od kiedy to :
z H2= d2 −a2 => Twój bbbb niepoprawny ( bzdurny) zapis na H
przecież
H= √d2−a2
:
z H2= d2 −a2 => Twój bbbb niepoprawny ( bzdurny) zapis na H
przecież
H= √d2−a2

 czyli w tym drugim zadaniu z trójkątem prawidłowym
bedzie tak:
czyli w tym drugim zadaniu z trójkątem prawidłowym
bedzie tak:
| a2√3 | ||
V = | * √d2 − a2 ?Na pewno można jeszcze to rozpisać, ale nie wiem jak...  | |
| 4 |
| DC` | ||
a przy liczeniu cosinusa, tak: cosα = | ? | |
| d |
| a2 | 4d2−3a2 | |||
IDC'I2= d2−a2 + | = | |||
| 4 | 4 |
| IDC'I | 1 | |||
cosα= | = | √4d2−3a2 | ||
| d | 2d |