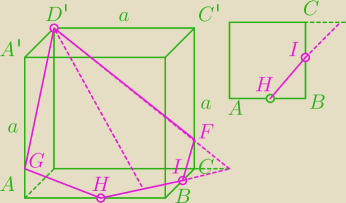
 nie jestem w stanie teraz wpisać rozwiązania,
może rysunek trochę rozjaśni
nie jestem w stanie teraz wpisać rozwiązania,
może rysunek trochę rozjaśni
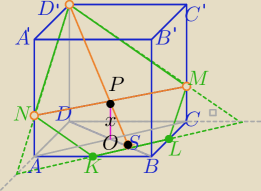 1) a− długość krawędzi sześcianu
d=|DB|=|AC|=a√2 długość przekątnej podstawy
1) a− długość krawędzi sześcianu
d=|DB|=|AC|=a√2 długość przekątnej podstawy
| 1 | 1 | |||
|KL|= | d, |OS|= | d, |MN|=a√2 | ||
| 2 | 4 |
| 3 | ||
2)W ΔD'DS: |D'S|2=a2+( | *a√2)2⇔ | |
| 4 |
| √34a | ||
|D'S|= | ||
| 4 |
| a | x | a | x | |||||||||||||||||
3) ΔPOS∼ΔD'DS⇔ | = | ⇔ | = | |||||||||||||||||
| DS | OS |
|
|
| 1 | ||
x= | a | |
| 3 |
| 1 | ||
|PS|2=(13a)2+( | a√2)2 | |
| 4 |
| √34a | ||
|PS|= | ||
| 12 |
| 1 | √34a | √34a | a2√17 | |||||
4) PΔMND'= | *a√2*( | − | )= | |||||
| 2 | 4 | 12 | 6 |
| a√2+0.5a√2 | √34a | a2√17 | ||||
PKLMN= | * | = | ||||
| 2 | 12 | 8 |
| a2√17 | a2√17 | |||
PKLMD'N= | + | |||
| 6 | 8 |
| 7a2√17 | ||
PKLMD'N= | ||
| 24 |