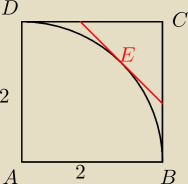
W kwadracie ABCD o boku długości 2 zawiera się łuk okręgu o środku w punkcie A i promieniu
AB. Rozważamy wszystkie odcinki spełniające jednocześnie dwa warunki:
1) Odcinek jest styczny do danego łuku w dowolnie wybranym na tym łuku punkcie E (E≠B
i E≠D)
2) Jeden koniec odcinka należy do boku BC, zaś drugi do boku DC
Wykaż ,że najkrótszy odcinek spełniający warunki zadania ma długość 4(√2−1)
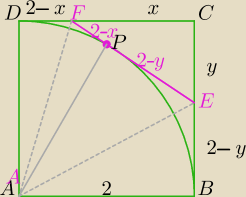ΔADF≡ΔAFP i ΔAPE≡ΔABE
0<x<2, 0<y<2
z tw. Pitagorasa dla ΔFCE
(2−x+2−y)2=x2+y2
xy−4x−4y+8=0
| 4y−8 | ||
x= | ||
| y−4 |
| 4y−8 | y2−4y+8 | |||
|FE|=2−x+2−y=2− | +2−y= | |||
| y−4 | 4−y |
| y2−4y+8 | ||
trzeba znaleźć minimum f(y)= | i sprawdzić, czy będzie równe podanej w zadaniu | |
| 4−y |