Ile wyrazów dodatnich ma ciąg określony wzorem an=-n^2+2n+24 franek: Ile wyrazów dodatnich ma ciąg określony wzorem an=−n²+2n+24

Satan: −n² + 2n + 24 = −(n² − 2n − 24) = −(n² − 2n + 1 − 25) = −(n − 1)² + 25 Czyli a_n = −(n − 1)² + 25 −(n − 1)² + 25 = 0 ⇒(n − 1)² = 25 ⇒|n − 1| = 5 ⇒ n = 6 v n = −4 Rysujesz wykres funkcji, sprawdzasz dla n > 0 i podajesz odpowiedź. Można też deltą, ale tak jest też łatwo.

Fra: (−nieskonczonosc,−4),(6,+nieskoczonosc) ?

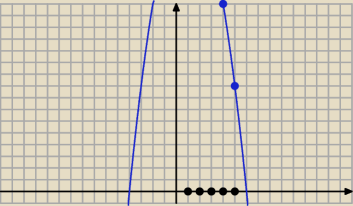
Janek191: n ∊ ( − 4, 6)∩ ℕ , czyli n ∊ { 1,2,3,4,5} Jest 5 dodatnich wyrazów tego ciągu. Patrz też na wykres