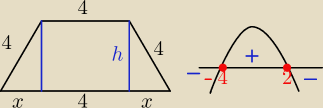Zadania optymalizacyjne, Planimetria. La gringa: Treść zadania: : Okno na poddaszu ma kształt trapezu równoramiennego, którego krótsza podstawa i ramiona mają długość po 4 dm Oblicz, jaką długość powinna mieć dłuższa podstawa tego trapezu, aby do pomieszczenia wpadało przez to okno jak najwięcej światła, czyli aby pole powierzchni okna było największe. Oblicz to pole. Prosiłbym o weryfikację, gdyż nie mam podanego rozwiązania, a chciałbym mieć pewność iż zadanie jest zrobione prawidłowo Zał. x>0; h>0;

	4+4+2x
P =		* h h2 = 16 − x2 ⇒ h=√16−x2 16−x2≥0 ⇒ x≤4 v x≥−4 ⇒ x ∊ (0,4>
	2

Tworzę funkcję opisującą pole tego trapezu:

	8+2x
f(x)=		*√16−x2
	2

f(x)=(4+x)*√16−x² Tworzę pochodną.

	1
f'(x)= 1 * (√16−x2) + (4+x)*		*(−2x)
	2*√16−x2

	−x
f'(x)= √16−x2 + (4+x)*
	√16−x2

	−2x2−4x+16
f'(x)=
	√16−x2

Wyznaczam ekstrema. Warunek konieczny:

	−2x2−4x+16
f'(x) = 0 ⇒		= 0
	√16−x2

−2x²−4x+16 = 0 Δ=144 √Δ=12 x₁ = 2 x₂ = −4 x₂ nie spełnia założeń. Rozważamy tylko x₁. Warunek wystarczający (zmiana znaku) rysunek powyżej. −Zmiana znaku następuje z + na −. Czyli x=2 jest naszym szukanym maksimum. ODP: Dłuższa podstawa trapezu powinna mieć długość: 4 + 2*2 = 8 Największe możliwe pole tego trapezu wynosi: (4+8):2 * √12 = 6√12 ⇒ 12√3

aniabb: ok