trapez jołłł246: W trapez ABCD , gdzie AB ∥ CD i |AB | > |CD | , wpisano okrąg. Dwusieczna kąta ostrego przy wierzchołku A jest prostopadła do ramienia |BC | . Wykaż, że dwusieczna kąta przy wierzchołku D jest równoległa do ramienia BC .

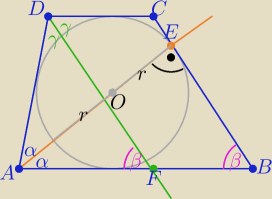
Eta: Dwusieczna kąta A zawiera promień okręgu 2α+2γ=180^o ⇒ α+γ=90^o i w ΔABE α+β=90^o to γ=β więc w ΔADF 2α+γ+|∡AFD|= 180^o ⇒2α+β+ |∡AFD|=180^o ⇒|∡AFD|= β to proste DF i BC tworzą z podstawą AB kąty o równych miarach β zatem DF ∥BC c.n.w