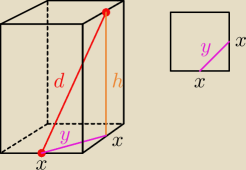
Zadania optymalizacyjne, Stereometria. La gringa: Odcinek łączący środki dwóch skośnych krawędzi podstaw graniastosłupa prawidłowego czworokątnego ma długość d=10. Jaką wysokość powinien mieć ten graniastosłup aby: 1) pole jego powierzchni bocznej było maksymalne? 2) pole jego powierzchni całkowitej było maksymalne?

Basia: 0 < h < 10 y² = (x/2)²+(x/2)² = (x²/4)+(x²/4) = 2x²/4 = x²/2 y²+h² = 10²

x2
	+h2=100
2

x²+2h²=200 x² = 200−2h² P_b = 4*x*h = 4h√200−2h² P_c = 2x²+P_b = 2(200−2h²) + 4h√200−2h² i szukasz maksimum tych funcji w przedziale (0,10) cyli pochodna i tak dalej

La gringa: 1) f(h) = 4h√200−2h² ⇒ 4√200h²−2h⁴ Obliczam pochodną:

	1
f'(h) = 4 *		* (400h − 8h3)
	2*√200h2−2h4

	−16h2+800
f'(h) =
	√200−2h2

Wyznaczam ekstrema. Warunek konieczny f'(h)=0 0=−16h² + 800 ... h₁=5√2 lub h₂=5√2 zał. h(0;10) czyli h₂ nie spełnia naszych założeń. Rozpatrujemy tylko h₁. Warunek wystarczający: zmiana znaku. Rysujemy wykres. Następuje zmiana z + na −. Czyli to jest nasze szukane maksimum. Odp. Dla h=5√2 Powierzchnia boczna będzie największa. Czy to rozwiązanie jest poprawne/a jeśli jest to w takiej formie byłoby poprawnie przedstawione na arkuszu maturalnym droga Basiu?

Basia: oczywiście poprawne tam przy h₁ brakuje minusa, ale rozumiem doskonale, że to tylko literówka natomiast nie bardzo rozumiem o co Ci chodzi z tym arkuszem może o opis? w rozwiązaniu na arkuszu powinno się naszkicować wykres licznika pochodnej i dodać krótkie uzasadnienie: mianownik jest stale dodatni więc znak pochodnej zależy tylko od licznika no i potem dokładniej rozpisać h∊(0,5{2})⇒ f'(h)>0 ⇒ f(h) rośnie h∊(5√2;10) ⇒ f'(h)<0 ⇒ f(h) maleje stąd dla h=5{2} f. osiąga maksimum to już na pewno wystarczy

La gringa: Bardzo dziękuję Teraz już mam pewność jak wykonywać takie zadania