:D poziomka: Zbadaj liczbę rozwiązań ze względu na wartość parametru m (m∊R). Napisz wzór i naszkicuj wykres funkcji y=g(m), która każdej wartości parametru m przyporządkowuje liczbę rozwiązań równania: (m−5)x²−4mx+m−2=0

Janek191: Jak się nie pomyliłem, to; ( m − 5) x² − 4 m x + m − 2 = 0 Dla m ≠ 5 Δ = 16 m² − 4*(m −5)*(m−2) = 16 m² − 4*(m² − 7 m + 10) = 16 m² − 4 m² + 28 m − 40 = = 12 m² + 28 m − 40 > 0 / : 4 3 m² + 7 m − 10 > 0 Δ_m = 49 − 4*3*(−10) = 49 + 120 = 169 √Δ_m = 13

	− 7 − 13		10
m =		= −		lub m = 1
	6		3

	1
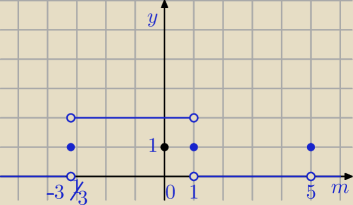
m ∊ (U{ − 3		, 1) − równanie ma 2 rozwiązania
	3

	1
m = − 3		lub m = 1 − równanie ma jedno rozwiązanie
	3

	1
Dla m ∊ ( − ∞, − 3		) ∪ ( 1, 5) ∪ ( 5, +∞) równanie nie ma rozwiązań
	3

Dla m = 5 równanie ma jedno rozwiązanie

poziomka: A mógłbyś mi wytłumaczyć jak narysowałeś wykres, bo mam problem z tym?