Zadanie maturalne - poziom rozszerzony, planimetria.
Nedar: Punkt D leży na boku AB trójkąta ABC, przy czym |AD| : |AB| = 2 : 5. Środkowa AS przecina
odcinek CD w punkcie P. Wyznacz |CP| : |PD|. Prosiłbym o pełne rozwiązanie wraz z rysunkiem.
18 kwi 15:35
Mila:
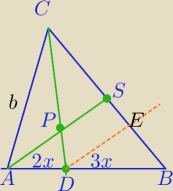
CB=a
1) DE||AS⇔
ramiona kąta B przecięte prostymi równoległymi
| SE | | 2 | | 1 | | 1 | |
| = |
| i |SE|+|EB|= |
| a ⇔|SE|= |
| a |
| EB | | 3 | | 2 | | 5 | |
2) ramiona kąta DCB przecięte prostymi równoległymi⇔
| CS | | SE | | PD | | SE | |
| = |
| ⇔ |
| = |
| ⇔ |
| CP | | PD | | CP | | CS | |
=================
Posprawdzaj rachunki
18 kwi 16:43
Eta:
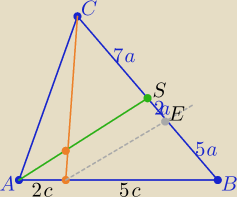
| |CP| | | 7a | | CP| | | 7 | |
| = |
| ⇒ |
| = |
| |
| |PD| | | 2a | | |PD| | | 2 | |
=========
18 kwi 19:30
Mila:
?
18 kwi 20:14
Eta:
Raaaaaaaaaacja przeczytałam |AD|: |DB|=2:5
18 kwi 20:19
Mila:
Tak myślałam, szkoda, że autorzy wrzucają zadania i na tym koniec.
Czasem mają odpowiedź w zbiorze, to niekiedy pomogłoby uniknąć pułapek.
18 kwi 20:25
18 kwi 20:30
Bogdan:
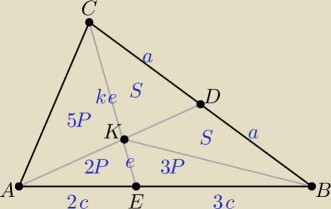
Inny sposób (na moim rysunku przyjąłem inne oznaczenia).
w − wysokość trójkątów AEK i AKC wychodząca z A oraz P, S − pola trójkątów.
Pola trójkątów: P
ABD = 2P + 3P + S = P
ADC = S + 5P
| | 1 | | 1 | | 5 | |
PAKC = |
| *ke*w = 5P i PAEK = |
| *e*w = 2P ⇒ k = |
| |
| | 2 | | 2 | | 2 | |
18 kwi 20:58
Eta:

18 kwi 21:02
 CB=a
CB=a



 w maju po maturze
w maju po maturze 
 Inny sposób (na moim rysunku przyjąłem inne oznaczenia).
w − wysokość trójkątów AEK i AKC wychodząca z A oraz P, S − pola trójkątów.
Pola trójkątów: PABD = 2P + 3P + S = PADC = S + 5P
Inny sposób (na moim rysunku przyjąłem inne oznaczenia).
w − wysokość trójkątów AEK i AKC wychodząca z A oraz P, S − pola trójkątów.
Pola trójkątów: PABD = 2P + 3P + S = PADC = S + 5P

