dsa das: Narysuj na płaszczyźnie zespolonej Im(z+i)⁴ ≤ 0 Jakąś wskazówke ktoś może?

das: Dam mi coś jak przejdę na postać trygonometryczną?

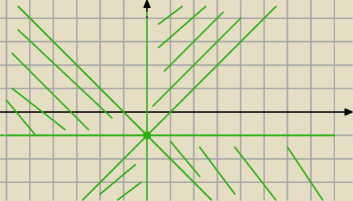
Pytający: Da, najpierw możesz podstawić: u=z+i=|r|(cos(φ)+i*sin(φ)) Im(u⁴)≤0 Im(|r|⁴(cos(4φ)+i*sin(4φ)))≤0 |r|⁴sin(4φ)≤0 sin(4φ)≤0 ∨ r=0 4φ∊<−π+2kπ, 2kπ>

	−π		kπ		kπ
φ∊<		+		,		>
	4		2		2

z=u−i, stąd rysunek

PW: Niech z=x+iy, wtedy z+i=x+i(y+1),

	4 1		4 2		4 3
(z+i)4=(x+i(t+1))4=x4+		x3i(y+1)+		x2i2(y+1)2+		xi3(y+1)3+i4(y+1)4=

=x⁴+4x³(y+1)i−6x²(y+1)²−4x(y+1)³i+(y+1)⁴. Im(z+i)⁴=4x³(y+1)−4x(y+1)³ Im(z+i)⁴≤0 ⇔ 4x³(y+1)≤4x(y+1)³ Rozwiązaniami nierówności są m.in. wszystkie pary (x,y), w których (1) x=0 lub y+1=0. Jeżeli x≠0 i y+1≠0, to równoważną nierównością jest (po podzieleniu stronami przez 4x²(y+1)²)

	x		y+1
		≤
	y+1		x

	x2−(y+1)2
		≤0
	x(y+1)

	(x−y−1)(x+y+1)
(2)		≤0.
	x(y+1)

Żeby to narysować, trzeba przeprowadzić analizę, np. 1° Jeżeli x>0 i (y+1)>0, to nierównośc (2) jest równoważna nierówności x−y−1≤0 (3) y≥x−1. 2° Jeżeli x<0 i (y+1)<0, to (2) jest równoważna nierówności x−y−1≥0 (4) y≤x−1 i tak dalej.

PW: Pytający, nie widziałem Twojego rozwiązania. \Wygląda na to, że z mniejszym polotem, ale dojdę do tego samego

Pytający: PW, można też powiedzieć, że to Ty napisałeś z większym polotem. A już na pewno z większym rozmachem.

PW: Nie żartuj sobie z wyrobnika. Muszę się przyznać, że mam taką wadę − jak już zacznę jakiś pomysł, to brnę do końca, żeby się przekonać, czy da się to zrealizować. Często z tego powodu w sytuacjach egzaminacyjnych brakowało mi czasu, niestety.