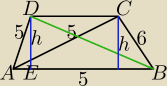
W trapezie ABCD o podstawach AB i CD dane są dlugości |AB|=|AC|=|AD|=5 i |BC|=6. Oblicz długość
przekątnej BD.
Wyznaczyłem pole trójkąta ABC ze wzoru Herona :
| 5+5+6 | ||
p= | =8 | |
| 2 |
| 1 | ||
12= | *5*h | |
| 2 |
| 24 | ||
h= | ||
| 5 |
| 24 | ||
|AE|2+ | =52 | |
| 5 |
| 7 | ||
|AE|= | ||
| 5 |
| 24 | 7 | |||
( | )2 + (5− | )2 =|DB|2 | ||
| 5 | 5 |
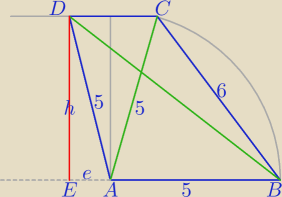Ten trapez inaczej wygląda, spróbuj narysować ( cyrkiel linijka).
1) PΔABC=12
| 24 | ||
h= | ||
| 5 |
