aa Mateusz: Narysuj wykres funkcji:

	|x|
f(x) =
	x−1

robię w przedziałach

	−1
a) (−∞,0) −> f(x) =		−1
	x−1

	1
b) <0, +∞) −> f(x) =		+1
	x−1

al nie wychodzi mi coś wykres zgodnie z odpowiedziami

Blee: to widać źle rysujesz bo funkcja dobrze przekształcona Pamiętaj także że x≠1

Mateusz: nie rozimiem czemu wykres w punkcie (0,0) odbija się i "idzie" w dół

Blee:

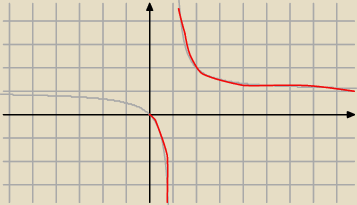
	x
bo jest to dodatnia część wykresu f(x) =
	x−1

Mateusz: nadal nie rozumiem

Blee: ale czego tutaj nie rozumiesz? rysujesz dwie funkcje ... ich 'połączenie' daje Ci wykres funkcji z wartością bezwzględną

Mateusz: tego co napisałem o 16:11 a rysunek niestety nie rozjaśnił

Blee: to już widzę, że to co napisałeś w pierwszym poście to jest po prostu to co zrobił ktoś inny, a Ty tylko zdołałeś to przepisać

Mateusz: Nie, wzory tych funkcji wyprowadziłem sam, ale jak rysuje to mój wykres się tak nie "załamuje" w punkcie (0,0)

Blee: to widać źle rysujesz

Mateusz: może teraz uda mi się załapać ideę

	1
mam wzór f(x)=		+1 dla x ∊ <0, +∞)
	x−1

z dziedziny wypada nam 1 więc robiąc sobie np tabelkę (x,y) powinienem wziąć jakąś licczbę z zakresu <0,1)? jakieś inne sugestie jak dość do wykresu z 16:17?

Blee: 1) narysuj h(x) = 1/x 2) przesun funkcje o wektor [1, 1] 3) interesuje Ciebie tylko to co jest na prawo od osi OY

Mateusz: tak robię, ale nie otrzymuję tego co Ty mam zwykłą hiperbole

Blee: Toc ja takze mam wykres hiperboli, ale interesuje nas tylko CZESC tego wykresu. Analogicznie czesc INNEJ hiperboli bedzie nas interesowala pozniej

Mateusz: okej, tę część mam

Mateusz: teraz rysować tę dla (−∞,0) , tak?

Mateusz:

Mateusz:

kochanus_niepospolitus: tak