największa i najmniejsza wartość funkcji
Szczeniak: Wyznacz największą i najmniejszą wartość funkcji f osiąganą w podanym przedziale <1;3>
f(x)=x2+2x
17 kwi 12:56
Jerzy:
Ustal dziedzinę i policz ekstrema lokalne.
17 kwi 12:58
Blee:
f(1) = ...
f(3) = ...
f'(x) = ...
i szukasz ekstremum
jeżeli ekstremum wewnątrz badanego przedziału to:
f(
x{ekstremum}) = ...
17 kwi 12:59
Jerzy:
f'(x) = 0 ⇔ x = 2 ( należy do przedziału) lub x = − 2
17 kwi 13:00
PW: Można bez pochodnej.
Znana jest nierówność: dla u>0
przy czym równość ma miejsce tylko dla u=1 (dowód polega na pokazaniu łatwej nierówności
kwadratowej).
| | x | |
Podstawiając u= |
| otrzymamy |
| | 2 | |
| | x | |
przy czym równość ma miejsce tylko dla |
| =1, czyli dla x=2. |
| | 2 | |
Tak więc f
min=f(2)=2.
Skoro jedynym ekstremum funkcji f dla x>0 jest minimum osiągane w punkcie 2, a f jest ciągła na
<1, 3>, to osiąga na tym przedziale maksimum w jednym z krańców przedziału.
| | 5 | | 15 | | 13 | | 5 | |
f(1)= |
| = |
| > |
| =f(3), a więc fmax=f(1)= |
| . |
| | 2 | | 6 | | 6 | | 2 | |
17 kwi 13:43
PW:
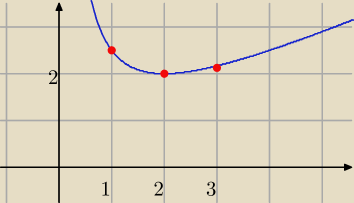
17 kwi 14:07
daras: a co nt blee

17 kwi 14:42
the foxi:
PW, kocham Twoje rozwiązania!

17 kwi 19:28
PW: Eeee

, mam takie hobby, żeby rozwiązywać − tam gdzie się da − metodami elementarnymi.
17 kwi 19:31



 , mam takie hobby, żeby rozwiązywać − tam gdzie się da − metodami elementarnymi.
, mam takie hobby, żeby rozwiązywać − tam gdzie się da − metodami elementarnymi.