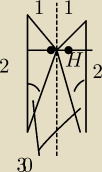
stereo mk: Hej, coś mi się nie zgadza w tym zadaniu, sprawdzi ktoś? W trójkącie prostokątnym jeden z kątów ostrych ma miarę 30, a przeciwprostokątna ma długość 2. Oblicz objętość bryły powstałej przez obrót trójkąta wokół prostej przechodzącej przez wierzchołek kąta prostego i równoległej do przeciwprostokątnej.

	√3
r będzie się równało
	2

	3π
Obliczyłam V walca V=		i odjełam od niej objętości stożków(jeden na górze, drugi na
	2

	√3		7π
dole) o r=		i ostatecznie wyszło mi V=		, a w odpowiedzi jest samo π
	2		8

Eta:

	1		2
V(bryły) =πr2*H −		πr2*H =		πr2*H
	3		3

	3
bo h1+h2=H=2 i r2=
	4

V= ..........=π

Eta:

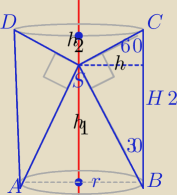Mila: V_walca=πr²*H |SC|=1 |BS|=√3 1*√3=2*h

	√3
h=		=r
	2

1)

	3		3π
Vwalca=π*		*2=
	4		2

2)

	1		3		π
Vstożka ABS=		π*		*h1=		*h1
	3		4		4

	1		3		π
Vstożka DCS=		π*		*h2=		*h2
	3		4		4

	3π		1π		1π		3π		π
Vfigury=		−(		h1+		h2)=		−		*(h1+h2)
	2		4		4		2		4

	3π		1π
Vfigury=		−		*2=π
	2		4

Eta: Coś nie tak Mila w moim ....

Mila: Nie widziałam Twojego wpisu. Jeśli Ci mój przeszkadza to usuń. Autorka i tak nie czyta.