Zadanie
Zuzia:
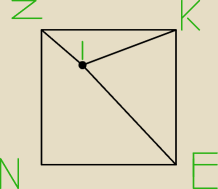
ZI:KI:EI=1:2:3 Oblicz miarę kąta ZIK
ZKEN − kwadrat
Punkt I jest dowolnym punktem wewnątrz kwadratu
Bardzo proszę o pełne rozwiązanie
16 kwi 20:24
Janek191:
a = I NE I
I ZE I = 4 I ZI I = a
√2
wiec
I ZI I = 0,25 a
√2
I KI I = 0,5
√2
Tw. kosinusów
| | 1 | | 1 | |
a2 = |
| *2 a2 + |
| *2 a2 − 2 *0,25 a√2*0,5 a√2 cos α |
| | 16 | | 4 | |
| | 1 | | 4 | | 1 | |
a2 = |
| a2 + |
| a2 − |
| a2 cos α / *8 |
| | 8 | | 8 | | 2 | |
8 a
2 = a
2 + 4 a
2 − 4 a
2 cos α
3 a
2 = − 4 a
2 cos α
16 kwi 20:36
Zuzia: Jak to ZI to a √2
16 kwi 21:04
Janek191:
Tam pisze, że I ZI I = 0,25 a
√2 
!
16 kwi 21:06
Zuzia: Ale ZE nie pokrywa się z przekątną
16 kwi 21:55