Trygonometria
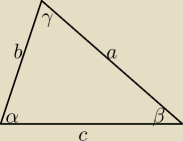
Piotr: α,β,γ to kąty trójkąta
Czy jeśli sin2α+sin2β=sin2γ to γ=90 stopni?
16 kwi 16:20
Blee:
y = 180 − (a+b)
sin2(180 − (a+b)) = sin2(a+b) = (sinacosb + cosasinb)2 =
= sin2acos2b + 2sinacosasinbcosb + sin2bcos2a
sin2a + sin2b = sin2acos2b + 2sinacosasinbcosb + sin2bcos2a
sin2a(1 − cos2b) + sin2b(1−cos2a) = 2sinacosasinbcosb
sin2asin2b + sin2asin2b = 2sinacosasinbcosb
sin2asin2b = sinacosasinbcosb
sinasinb = cosacosb
sin2asin2b = cos2acos2b
sin2asin2b = 1 − sin2a − sin2b + sin2asin2b
sin2a + sin2b = 1 ⇔ sin2b = cos2a ⇔ a + b = 90o
16 kwi 16:45
Blee:
napewno jest szybsza metoda
16 kwi 16:45
g: Po podstawieniu γ=180−α−β i przekształceniach wychodzi
sinα sinβ cos(α+β) = 0
Zatem raczej γ=90.
16 kwi 16:49
Bogdan:
| | a | | b | | c | |
Z twierdzenia sinusów: sinα = |
| , sinβ = |
| , sinγ = |
| |
| | 2R | | 2R | | 2R | |
| | a2 | | b2 | | c2 | |
sin2α + sion2β = sin2γ ⇒ |
| + |
| = |
| |
| | 4R2 | | 4R2 | | 4R2 | |
stąd a
2 + b
2 = c
2, zatem trójkąt jest prostokątny, przeciwprostokątną jest c, więc γ = 90
o
16 kwi 17:09
