16 kwi 07:22
Sebastian Porowski: Przesyłam swoje obliczenia :zadanie 4
Rozłozyłem wieloman do postaci (x−4)(x2−2)
otrzymałem x1=4 oraz x2 = −√2 i x3=√2
nastepnie wypisałem krotoność
x1 =1 oraz x2=1
czy to jest dobrze zrobione?
16 kwi 07:48
Blee:
Dobrze.
16 kwi 07:58
Blee:
W 3) wyciagasz x2 przed nawias
16 kwi 07:59
Blee:
Ale w (4) to jeszcze nie koniec ... musisz zrobic 'wezyka' i podac przedzialy kiedy ta funkcja
jest mniejsza od 0
16 kwi 08:00
Blee:
W (3) zrob podstawienie: t = x3 i rozloz na czynniki, pozniej wracasz z podstawieniem i dalej
rozkladasz (stosujac wzory skroconego mnozenia)
16 kwi 08:01
Sebastian Porowski: zadanie 3
po rozłozeniu na cyznnii doszedłem do postaci
x2(x+2)(x+6)=0
wyliczyłem z tego
x2=0
x1= −6
x2=−3
x3=0 czy to poprawne rozwiązanie?
16 kwi 08:01
Blee:
Tfu ... w (2) to podstawienie
16 kwi 08:01
Blee:
Rozlozone zle:
x2(x2 − 8x + 12) = x2(x−2)(x−6)
16 kwi 08:03
Blee:
A nawet jakbys mial dobrze to skad to x2 = −3 sie pojawilo?
16 kwi 08:04
Sebastian Porowski: jak zrobić tego wężyka?
16 kwi 08:05
Sebastian Porowski: wybacz pomyłka x2=−2
16 kwi 08:06
16 kwi 08:07
Sebastian Porowski: aha czyli w przypadku tego rozozenia wyniki to
x1=2, x2=6 , x3=0?
16 kwi 08:08
Sebastian Porowski: jak rozwiązać 2i 5 mówiąc szczerze tutaj nie mam pomysłu,co do węzyka dzięki za info już wiem
jak to zrobić ,dzięki za link
16 kwi 08:12
Blee:
(2) napisalem: podstawienie t= x3
Wtedy masz t2 + 7t − 8 = (t+8)(t−1)
Wracasz z podstawieniem:
(x3+8)(x3−1)
I teraz stosujesz wzory skroconego mnozenia:
a3 + b3 = (a+b)(a2 −ab +b2)
a3 − b3 = (a−b)(a2 + ab + b2)
16 kwi 08:15
Blee:
Co do (5) to tutaj niestety trzeba pokombinowac i mozna to zrobic na dwa sposoby:
1) szukamy calkowitych pierwiastkow, calkowitymi pierwiastkami moga byc tylko te liczby ktore
dziela wyraz wolny (3)
Wiec mamy tylko takie mozliwosci: +1, −1, +3, −3
Podstawiamy kolejno kazda z nich i sprawdzamy czy ktorys jest pierwiastkiem (bedzie x= −1)
16 kwi 08:18
Blee:
Drugi sposob to probujemy to rozlozyc − i tutaj na dobra sprawe niestety istotna jest wprawa i
'kombinowanie'
16 kwi 08:19
Sebastian Porowski: jak zastosowac te wzory? jak to powinno wyglądac?
a nie moge po prostu wyliczyc pierwiastka 3 stopnia z 8?
i wtedy wyjdzie mi x1=2 oraz w x 2 wyjdzie mi 1 ?
16 kwi 08:22
Sebastian Porowski: oki jeszcze jedno pytanie w 6 wyszlo mi cos takiego w mianowniku skrociłem pierwiastki z
potegami i powstało
x2−4x
rozłozyłem to na (x−2)(x+2)
df =2 i −2?
16 kwi 08:26
Blee:
Pierwiastki wtjda −2 i +1 ale dopiero po rozlozeniu wiesz ze wiecej nie ma
16 kwi 08:27
Blee:
x
4 − 4x
2 pod zadnym pozorem nie jest rowne (x
2−4x)
2 
Nie mozesz tak zrobic
16 kwi 08:29
Sebastian Porowski: hmm ok to kombinuje dalej jak ogarnąć zadanie 6
16 kwi 08:31
Blee:
Skoro masz pierwiastek i ulamek to:
1)
√to co jest tutaj musi byc ≥0
| | . | |
2) |
| |
| | to co jest tutaj musi byc ≠ 0 | |
Czyli w tym przypadku wyrazenie pod pierwiastkiem musi byc >0
Wiec rozwiazujesz x
4 − 4x
2 >0
I robisz tak jak (4) −−− czyli rozkladasz a pozniej wezykiem
16 kwi 08:32
Sebastian Porowski: w 6 postać po rozłożeniu to
x2(x−4)>0
wtedy x1=0
x2=4?
16 kwi 14:43
Sebastian Porowski: czyli w 6 pierawiastki to x1=0 i x2=4 krotnosc dla pierwiastka x1 dwa? a dla ego drugiego
krotnosc to jeden?
16 kwi 14:46
ite:
6/ x4−4x2=x2(x2−4)=x2(x−2)(x+2)
czyli szukaj rozwiązań nierówności x2(x−2)(x+2)>0
16 kwi 15:06
Sebastian Porowski: dzięki wielkie ITE dziś będę dalej nad tym siedział to wrzuce wynik
choc wydaje mi sie ze rozwiazanie tej niewrownosci to
x1=0 x1=2 x2=−2 ,dobrze musle?
16 kwi 15:33
ite:
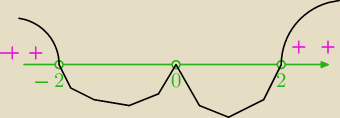
rozwiązaniem równania byłyby liczby x
0=−2, x
1=0, x
3=2
ale tutaj jest
nierówność
(x+2)x
2(x−2)>0
16 kwi 15:43
Sebastian Porowski: czyli odpada mi x1=01 ,poniewaz założenia nierownosci wynika ,że to po lewej stronei wszystko
musi byc wieksze od zera?
16 kwi 15:49
Sebastian Porowski: x1=0
16 kwi 15:49
ite:
tak zero odpada, podstaw do wzoru funkcji, i sprawdź, czy działanie jest wykonalne
16 kwi 15:52
Sebastian Porowski: tylko patrzac na to odpada mi też dwa ,jeśli podstawie dwa za x
to mam (2+2)*22(2−2)>0
4*4*0>0
0>0 a to nie prawda
Czyli rozwiązaniem tej nierówność jest tylko x1=−2 ?
16 kwi 15:56
Sebastian Porowski: tylk oznowu jak do tej nierównosci podstawie −2 to też mi wychodzi zero.Czy coś robię źle? tak
samo jak podstawie te liczby do wzoru funkcji też mi wszędzie tam wychodzi 0
16 kwi 16:02
ite:
rozwiązaniem tej nierówności jest suma przedziałów zaznaczonych plusami (−∞,−2)U(2,∞)
ani −2 ani 2 nie należą do zbioru rozwiązań (procedura tak jak z zerem, podstaw, jeśli masz
wątpliwości)
16 kwi 16:04
Sebastian Porowski: oki teraz juz załapałem dziękuje za pomoc oraz cierpliwość. Mam jeszcze jedno pytanie jak
ruszyć pierwsze zadanie?
16 kwi 16:08
ite:
skoro liczby 1 i −2 są pierwiastkami wielomianu W(x)= 3x3+ax2+bx+4, to W(1)=0 i W(−2)=0
wstaw do wzoru wielomianu w miejsce x najpierw jedną potem, drugą liczbę
otrzymasz dwa równania z dwiema niewiadomymi a i b
rozwiąż je
16 kwi 16:27
Sebastian Porowski: Podstawiam osobno 1 do wzoru a nastepnie do wzoru podstawiam −2 i rozwiazuje układ równan z
,którego wyliczam a i b
16 kwi 17:57
iteRacj@:
W(1)=0 czyli 3*13+a*12+b*1+4=0
W(−2)=0 czyli 3*(−2)3+a*(−2)2+b*(−2)+4=0
z tego ukłdu wyliczasz a i b
16 kwi 21:16
