Zdarzenia, zadanie na wykazanie

Zdarzenia, zadanie na wykazanie KOKO: Niech A,B będą zdarzeniami losowymi zawartymi w Ω. Wykaż, że jeśli P(A∩B)=P(A)P(B), to P(A∩B')=P(A)P(B')

15 kwi 20:43

Eta:

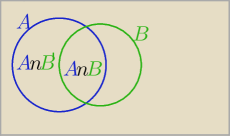
A∩B^' = A\ (A∩B) i P(A∩B)=P(A)*P(B) i 1−P(B)= P(B^') to L=P(A∩B^')= P(A)−P(A∩B) = P(A)− P(A)*P(B) = P(A)[1−P(B)] = P(A)*P(B^')=P

15 kwi 20:53

KOKO: Dzięki!

15 kwi 21:02

αβγδπΔΩ∞≤≥∊⊂∫←→⇒⇔∑≈≠innerysuję

Φεθλμξρςσφωηϰϱ

∀∃∄∅∉∍∌∏⊂⊄⊆⊃⊅⊇≡

∟∠∡∥∬∭∮∼⊥⋀⋁∩∪∧∨¬±

ℂ℃℉ℕℙℚℛℤℯ

↑↓↔↕↖↗↘↙△□▭▯▱◯⬠⬡

♀♂♠♣♥♦

imię lub nick

zobacz podgląd

wpisz,
a otrzymasz

Kliknij po więcej przykładów
5^2	5²
2^{10}	2¹⁰
a_2	a₂
a_{25}	a₂₅
p{2}	√2
p{81}	√81
Twój nick