K Kasia:

	1
Wyznacz rownanie etycznej do wykresu funkcji		x4−1
	2

	5
Przechodzącej przez punkt (0,−		)
	2

	5
Wyznaczyłam pochodną, wiem, ze prosta ma rownanie y=ax−		, ale nie wiem jak A policzyc
	2

iteRacj@: współczynnik kierunkowy a prostej jest równy wartości pochodnej w punkcie styczności

Basia:

	5
punkt (0;		) nie należy do wykresu funkcji
	2

więc to co napisałaś ]P[iteRacj@]] nie wystarcza

Kasia: Więc jak mam to zrobić?

iteRacj@: tak, mój błąd

Basia: y = ax+b

5
	= a*0+b
2

	5
b =
	2

	5
y = ax+
	2

	1
f(x) =		x4−1
	2

	1
f'(x) =		*4x3 = 2x3
	2

i szukamy punktu styczności czyli takiego x, dla którego a = 2x³ oraz wartość funkcji = wartości funkcji liniowej, której wykresem jest styczna

	5		1
ax+		=		x4−1
	2		2

	5		1
2x4+		=		x4−1
	2		2

no i albo coś sknociłam, albo idiotyzm wychodzi

3		7
	x4 = −
2		2

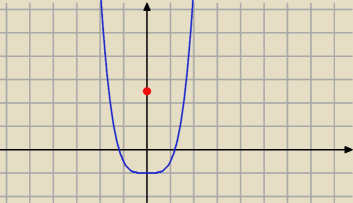
a to jest niemożliwe; nie sknociłam; taka styczna nie istnieje widać na wykresie żadna prosta, przechodząca przez (0; (5/2)) nie będzie styczna do wykresu tej funkcji może miał być inny wzór funkcji, albo inny punkt

Basia:

	5
jednak sknocilam; tam jest −
	2

niedowidzę zasada taka sama

Basia: będzie

	5		1
2x4 −		=		x4−1
	2		2

3		3
	x4 =
2		2

x⁴ = 1 ⇔ x²=1 ⇔ x=1 lub x=−1 czyli bedą dwie takie styczne

	5
dla x=1 ,mamy a = 2 czyli y = 2x−
	2

	5
dla x=−1 mamy a=−2 czyli y = −2x−
	2

Kasia: Dziękuję bardzo, po raz kolejny mnie ratujesz