Stereometria
Gustavo: Szescian o krawędzi długosci a przecięto płaszczyzną przechodzącą przez przekątną podstawy i
nachyloną do płaszczyzny pod kątem a.
a) Oblicz tangens największego z kątów a, dla którego przekrój ten jest trójkątem. Zaznacz ten
kąt wraz z odpowiednim przekrojem na rysunku.
b) Otrzymany przekój jest trójkątem. Oblicz pole tego trójkąta, wiedząc, że płaszczyzna, w
której jest on zawarty podzieliła szescian na dwie bryły, których stosunek objętosci wynosi
1:11.
15 kwi 20:11
iteRacj@:
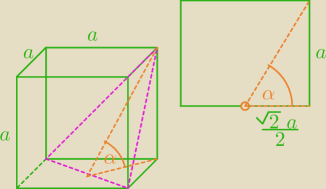
Jeśli w treści jest: przecięto płaszczyzną przechodzącą przez przekątną podstawy i
nachyloną do płaszczyzny
podstawy, to podpunkt przedstawia taka sytuacja
15 kwi 20:51
Gustavo: Własnie problem w tym, że w tresci nic o podstawie nie ma. Przypuszczam, że o podstawę chodzi.
15 kwi 20:56
iteRacj@:
albo o drugą podstawę (tę "na górze") i wtedy nic się nie zmienia
albo płaszczyznę ściany którejś bocznej
i tak się można domyslać...
15 kwi 21:08
iteRacj@:
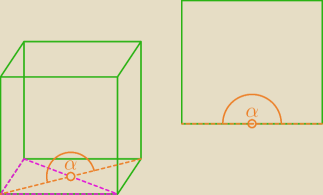
czy mój pomysł ma sens? najwiekszy kąt α=180
o ? ? ?
15 kwi 21:16
Mila:
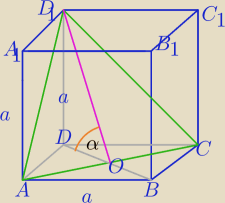
a) |DB|=a
√2
α
0≈54,7
o − największy kąt dla którego przekrój jest trójkątem
dla α∊(0,α
0> przekrój jest trójkątem równoramiennym.
15 kwi 21:26
Mila:
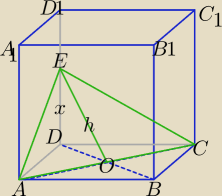
b)
Licz dalej sam.
15 kwi 21:37
Gustavo: Oki, dzięki
15 kwi 22:22
 Jeśli w treści jest: przecięto płaszczyzną przechodzącą przez przekątną podstawy i
nachyloną do płaszczyzny podstawy, to podpunkt przedstawia taka sytuacja
Jeśli w treści jest: przecięto płaszczyzną przechodzącą przez przekątną podstawy i
nachyloną do płaszczyzny podstawy, to podpunkt przedstawia taka sytuacja
 czy mój pomysł ma sens? najwiekszy kąt α=180o ? ? ?
czy mój pomysł ma sens? najwiekszy kąt α=180o ? ? ?
 a) |DB|=a√2
a) |DB|=a√2
 b)
b)