Dla jakich wartości x funkcja pochodna się zeruje?
Kalafiorarz: Dla jakich wartości x funkcja pochodna wynosi 0?
Mam tutaj pochodną
Gdy przyrównuje ją do 0 mnożę przez (x−1)
2, ponieważ nie tracę rozwiązania a otrzymuję 1=0
15 kwi 19:45
Basia:
ułamek = 0 ⇔ licznik = 0
x2−2x=0
x(x−2)=0
x=0 lub x=2
o ile należą do dziedziny funkcji, ale zapewne tak
15 kwi 19:48
Kalafiorarz: Dziękuję,
| | x2 | |
mam funkcję f(x) = |
| |
| | x−1 | |
więc należą
15 kwi 19:53
Blee:
jeżeli masz jeszcze określić monotoniczność funkcji f(x) to wtedy przydaje się wskazówka, którą
dostałeś wcześniej (o nie skracaniu mianownika w pochodnej)
ponieważ mianownik w tejże pochodnej będzie zawsze liczbą dodatnią (więc o znaku pochodnej mówi
nam licznik).
15 kwi 19:55
Kalafiorarz: i maksymalna wartość funkcji f(x) jest dla x=2 wtedy f(x)=4.
Mogę jeszcze zapytać o określanie monotoniczności?
Wnioskuję z tego, co przedstawia wykres, że powinienem wliczyć dziedzinę?
Bo w x=1 jest asymptota pionowa, więc funkcja rośnie dla x∊(−∞, 0) U (1, ∞)
maleje dla x∊(0, 1)
osiąga swoje minimum dla x=0, maksimum dla x=2 (?)
15 kwi 20:16
Blee:
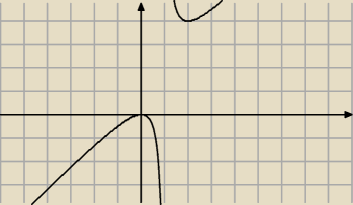
" i maksymalna wartość funkcji f(x) jest dla x=2 wtedy f(x)=4." <−−− bzduuura

15 kwi 20:29
Basia:
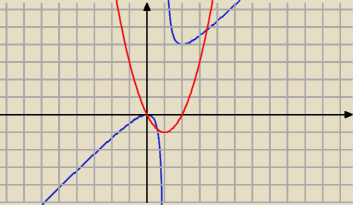
funkcja
nie rośnie w zbiorze (−
∞;0)∪(1,+
∞)
niebieskie to wykres funkcji
czerwone to wykres y = x
2−2x czyli
licznika pochodnej
mianownik jest stale dodatni
znak pochodnej zależy
tylko od licznika
x∊(−
∞;0) ⇒ f'(x)>0 ⇒ f rośnie
x∊ (0,1) ⇒ f'(x)<0 ⇒ f maleje
x∊(1;2) ⇒ f'(x)<0 ⇒ f maleje
x∊(2;+
∞) ⇒ f'(x)>0 ⇒ f rośnie
w p−cie x
1=0 ma maksimum lokalne = 0
w p−cie x
2=2 ma minimum lokalne = 4
nie wolno napisać, że maleje dla x∊(0;1)∪(1;2)
bo to nieprawda; popatrz na wykres
15 kwi 20:33
Kalafiorarz: W sensie f(2)=4, a pozostałe wypociny są dobrze ?
15 kwi 20:33
Basia: masz wyżej odpowiedź
15 kwi 20:35
Kalafiorarz: Bardzo dziękuję.
15 kwi 20:36
Kalafiorarz: à propos "nie wolno napisać, że maleje dla x∊(0;1)∪(1;2)
bo to nieprawda; popatrz na wykres"
czyli muszę zapisać
x∊ (0,1) ⇒ f(x) maleje
x∊(1;2) ⇒ f(x) maleje
15 kwi 20:47
 " i maksymalna wartość funkcji f(x) jest dla x=2 wtedy f(x)=4." <−−− bzduuura
" i maksymalna wartość funkcji f(x) jest dla x=2 wtedy f(x)=4." <−−− bzduuura 
 funkcja nie rośnie w zbiorze (−∞;0)∪(1,+∞)
niebieskie to wykres funkcji
czerwone to wykres y = x2−2x czyli licznika pochodnej
funkcja nie rośnie w zbiorze (−∞;0)∪(1,+∞)
niebieskie to wykres funkcji
czerwone to wykres y = x2−2x czyli licznika pochodnej