Oblicz obwod trapezu Karoooool: Kąty ostre trapezu mają miary α,β a długosci boków równoległych a,b i (a>b). Oblicz obwód trapezu.

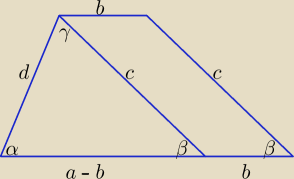
Bogdan: sinγ = sin[180^o − (α + β)] = sin(α + β)

	c		a − b		d		a − b
Z twierdzenia sinusów:		=		i		=
	sinα		sin(α + β)		sinβ		sin(α + β)

Basia:

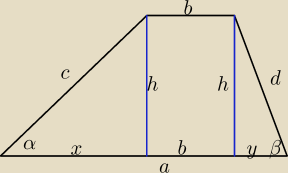
	h		h
tg α=		⇒ x =
	x		tg α

	h		h
tg β=		⇒ y =
	y		tg β

x+b+y = a x+y = a−b

h		h
	+		= a−b
tg α		tg β

	1		1
h(		+		) = a−b
	tg α		tg β

	tg β + tg α
h*		= a−b
	(tg α)*(tg β)

	(a−b)*(tg α)*(tg β)
h =
	tg β + tgα

	h
sin α =
	c

	h		(a−b)*(tg α)*(tg β)
c =		=
	sin α		(sin α)*(tg β + tg α)

d analogicznie

Karoooool: Dziekuje bardzo