| 8 | ||
Vs≤ | Vk. | |
| 27 |
| 4 | ||
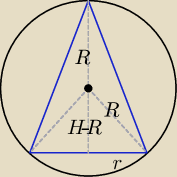
Objętość kuli Vk = | πR3 | |
| 3 |
| 1 | 1 | 1 | 2 | |||||
Objętość stożka Vs = | πr2H = | πH(2HR − H2) = − | πH3 + | πRH2 | ||||
| 3 | 3 | 3 | 3 |
| 4 | ||
Wyznaczamy maksimum funkcji Vs(H): Vs'(H) = −πH(H − | R) | |
| 3 |
| 4 | ||
Stożek wpisany w kulę o promieniu R ma największą objętość dla H = | R | |
| 3 |
| 32 | 8 | 4 | 8 | |||||
Vs max = | πR3 = | * | πR3 = | Vk | ||||
| 81 | 27 | 3 | 27 |