Oblicz Pc i V ostrosłupa czwokątnego oraz graniastosłupa sześciokątnego.
Paulinka;): Witam,
prosiłabym o rozwiązanie tych zadania, ponieważ jest to dla mnie syzyfowa praca, nie potrafię
tego wykonać, a jak już jestem blisko końca to wszystko się sypie.
1.W ostrosłupie prawidłowym czworokątnym ściana boczna jest nachylona do podstawy pod kątem
30°.
Krawędź podstawy ma długość 6. Oblicz Pc i V.
2.W graniastosłupie prawidłowym sześciokątnym najdłuższa przekątna długość 12 jest nachylona do
podstawy 60°
Oblicz Pc i V.
15 kwi 18:14
DM: W czym jest problem dokładnie?
15 kwi 18:39
Paulinka;): Szczerze ? We wszystkim .... Nie wiem jak się za to zabrać. Nie mam żadnego zadania tego typu
zrobionego żeby móc się wzorować, więc wiem że to co próbuję zdziałać jest... złe

Matematyka dla mnie jest straszna

15 kwi 18:42
DM:
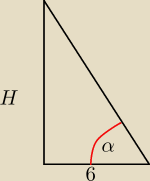
Wybacz za kiepski rysunek, ale nie mam wprawy w rysowaniu na tej stronce xD
tg(α) = H/6
tg(30 st) = H/6
.... wylicz H i V już możesz policzyć
a co do powierzchni ściany bocznej to jest to trójkąt od podstawie 6 i wysokości z
przeciwprostokątnej na tym niezdarnym rysunku co zrobiłem. Jak wyliczysz H to mozesz ją
policzyć
z tw. pitagorasa.
15 kwi 18:52
DM: Poprawka ten bok na dole ma mieć wartość "3".
15 kwi 18:54
DM: H =
√3
Pp = 6
2
V =
13Pp*H =
13*36*
√3
(
√3)
2 + 3
2 = d
2
3 + 9 = d
2
12 = d
2
2
√3 = d
Ps = 2
√3 * 6 *
12
Pc = Pp + 4Ps
Pc = 36 + 4*(6*
√3)
15 kwi 19:24
Mila:
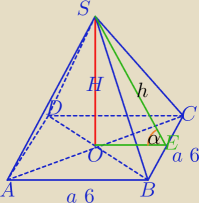
|OE|=3, α=30
| | 1 | | 1 | |
V= |
| *a2*H , Pc=a2+4* |
| *a*h=62+2*6*h |
| | 3 | | 2 | |
1) W ΔSOE:
| | H | | √3 | | H | |
tg30o= |
| ⇔ |
| = |
| ⇔ |
| | 0.5a | | 3 | | 3 | |
H=
√3
h
2=3
2+(
√3)
2⇔h
2=9+3=12
h=2
√3
2)
V=12
√3
========
3)
P
c=36+2*6*2
√3
P
c=36+24
√3
=========
15 kwi 19:38
Paulinka;): Jeszcze pytanko , to zadanie poniżej obliczam w ten sam sposób co obliczyłeś to przed chwilką?
Czy coś muszę zmienić i inaczej... ?
3. ) W ostrosłupie prawidłowym czworokątnym KRAWĘDŹ boczna jest nachylona do podstawy pod kątem
60°.
Krawędź podstawy ma długość 8. Oblicz Pc i V.
15 kwi 19:40
Paulinka;): Jesteście kochani, dziękuję Wam najmocniej. Ratujecie mnie

Jeszcze jakby ten graniastosłup szcześciokątny obliczyć to byłoby już w ogole bomba

Jeszcze raz wam dziękuję, jesteście wielcy !

Mądre główki

15 kwi 19:42
DM:
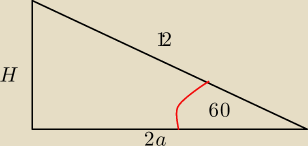
W drugim jest coś takiego, przy czym:
H − to wysokość graniastosłupa
2a − to dłuższa przekątna podstawy
a − to bok trójkąta równobocznego z których składa się podstawa graniastosłupa
15 kwi 19:58
DM:
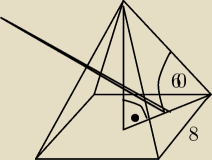
Rys do 3). Powinnaś dać sobie rade.
15 kwi 20:06
Mila:
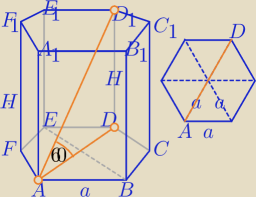
|AD
1|=12, |AD|=2a
V=P
6−kąta*H
P
c=2*P
6−kąta+6*a*H
1) W ΔADD
1: Δ ekierkowy (90,60,30)
|AD|=2a, |AD
1|=12=4a⇔,a=3
2)
| | a2√3 | | 32√3 | | 27√3 | |
P6−kąta=6* |
| =6* |
| = |
| |
| | 4 | | 4 | | 2 | |
V=243 [j
3]
=======
| | 27√3 | |
Pc=2* |
| +6*3*6√3=27√3+108√3 |
| | 2 | |
P
c=135
√3 [j
2]
============
15 kwi 20:46
Paulinka;): Mila jesteś najlepsza ! <3
A powiedz mi w tym zad. 1 , dlaczego wyszło h2=32+(√3)2⇔h2=9+3=12 h=2√3 ?
W sensie jak wyliczyłaś, że h = 2√3 ? Nie umiem dojść do tego

Matematyka to naprawdę dla mnie czarna magia

Dziękuję Ci najmocniej
15 kwi 20:50
Mila:
h2=12
h=√12=√4*3=√4*√3=2√3
15 kwi 21:12
Paulinka;): A w graniastosłupie skąd wiemy, że |AD1| wynosi 4a, a |AD| 2a?
|AD|=2a, |AD1|=12=4a⇔,a=3
15 kwi 21:14
Paulinka;): Racja

15 kwi 21:15
Paulinka;): Jeszcze mam dwa:
3.) W ostrosłupie prawidłowym czworokątnym KRAWĘDŹ boczna jest nachylona do podstawy pod kątem
60°.
Krawędź podstawy ma długość 8. Oblicz Pc i V.
4.) W ostrosłupie prawidłowym trójkątnym krawędź boczna jest nachylona do podstawy pod kątem
30°.
Krawędź podstawy ma długość 12. Oblicz Pc i V.
15 kwi 21:18
DM: Paulinka, przeanalizuj te dwa zadanka które masz już rozwiązane i spróbuje zrobić samodzielnie.
3) i 4) naprawdę nie różnią się tak bardzo od 1) i 2) a czego się nauczysz jak ktoś zrobi
wszystkie za Ciebie?
15 kwi 21:30
ford:
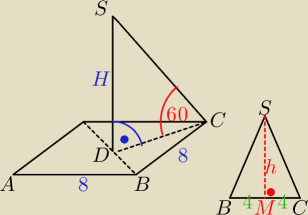
Zad. 3 z godz. 21:18
|DC| to połowa przekątnej kwadratu ABCD o boku 8
wzór na przekątną kwadratu o boku a to d=a*
√2
| | 1 | |
d = 8*√2 zatem |DC| = |
| *8√2 = 4√2 |
| | 2 | |
w ΔDSC:
| | H | |
√3 = |
| → H = 4√6, w tym momencie mamy wszystko do policzenia V |
| | 4√2 | |
| | |DC| | | 1 | | 4√2 | |
cos60o = |
| → |
| = |
| → |CS| = 8√2 |
| | |CS| | | 2 | | |CS| | |
w ΔSMC (Pitagoras): |SM|
2 + |MC|
2 = |CS|
2
h
2 + 4
2 = (8
√2)
2
h
2 + 16 = 128 → h
2 = 112 → h =
√112
w tym momencie mamy wszystko do policzenia Pc.
V = P
p*H = 8
2 * 4
√6 = 64 * 4
√6 =
256√6
P
c = P
p + 4P
b
| | 1 | | 1 | |
Pb = |
| a*h = |
| *8*√112 = 4√112 |
| | 2 | | 2 | |
Pc = 8
2 + 4*4
√112 = 64+16
√112 = 64+16
√16*7 =
64+64√7
15 kwi 21:31
 Matematyka dla mnie jest straszna
Matematyka dla mnie jest straszna
 Wybacz za kiepski rysunek, ale nie mam wprawy w rysowaniu na tej stronce xD
tg(α) = H/6
tg(30 st) = H/6
Wybacz za kiepski rysunek, ale nie mam wprawy w rysowaniu na tej stronce xD
tg(α) = H/6
tg(30 st) = H/6
 |OE|=3, α=30
|OE|=3, α=30
 Jeszcze jakby ten graniastosłup szcześciokątny obliczyć to byłoby już w ogole bomba
Jeszcze jakby ten graniastosłup szcześciokątny obliczyć to byłoby już w ogole bomba  Jeszcze raz wam dziękuję, jesteście wielcy !
Jeszcze raz wam dziękuję, jesteście wielcy !  Mądre główki
Mądre główki 
 W drugim jest coś takiego, przy czym:
H − to wysokość graniastosłupa
2a − to dłuższa przekątna podstawy
a − to bok trójkąta równobocznego z których składa się podstawa graniastosłupa
W drugim jest coś takiego, przy czym:
H − to wysokość graniastosłupa
2a − to dłuższa przekątna podstawy
a − to bok trójkąta równobocznego z których składa się podstawa graniastosłupa
 Rys do 3). Powinnaś dać sobie rade.
Rys do 3). Powinnaś dać sobie rade.
 |AD1|=12, |AD|=2a
V=P6−kąta*H
Pc=2*P6−kąta+6*a*H
1) W ΔADD1: Δ ekierkowy (90,60,30)
|AD|=2a, |AD1|=12=4a⇔,a=3
|AD1|=12, |AD|=2a
V=P6−kąta*H
Pc=2*P6−kąta+6*a*H
1) W ΔADD1: Δ ekierkowy (90,60,30)
|AD|=2a, |AD1|=12=4a⇔,a=3
 Matematyka to naprawdę dla mnie czarna magia
Matematyka to naprawdę dla mnie czarna magia  Dziękuję Ci najmocniej
Dziękuję Ci najmocniej

 Zad. 3 z godz. 21:18
|DC| to połowa przekątnej kwadratu ABCD o boku 8
wzór na przekątną kwadratu o boku a to d=a*√2
Zad. 3 z godz. 21:18
|DC| to połowa przekątnej kwadratu ABCD o boku 8
wzór na przekątną kwadratu o boku a to d=a*√2