KOMBINATORYKA bluee: Oblicz ile jest liczb dwunastocyfrowych zapisanych wyłącznie za pomocą cyfr 1,2,3 i takich, że każde dwie sąsiednie cyfry różnią się o 1.

ford: niech x = {1,3} czyli do zbioru x należą dwie liczby: 1 i 3 rozważamy trzy przypadki I. 12x2x2x2x2x2 − czyli liczba zaczyna się jedynką, potem musi być dwójka, potem x (czyli 1 lub 3), potem dwójka, potem x itd. ilość sposobów = 1*1*2*1*2*1*2*1*2*1*2*1 = 32 II. 2x2x2x2x2x2x − czyli liczba zaczyna się dwójką, potem x (czyli 1 lub 3), itd. ilość sposobów = 1*2*1*2*1*2*1*2*1*2*1*2 = 64 III. 32x2x2x2x2x2 − liczba zaczyna się trójką, potem dwójka, potem x (1 lub 3), itd. ilość sposobów = 1*1*2*1*2*1*2*1*2*1*2*1 = 32 32 + 64 + 32 = [P[128] liczb

bluee: Mam jeszcze takie cudo: Kuba próbował się dodzwonić do serwisu komputerowego. Znał wszystkie cyfry numeru telefonu z wyjątkiem ostatniej i dlatego wybierał ją przypadkowo (za każdym razem inną). Oblicz prawdopodobieństwo, że uzyskał połączenie z serwisem najpóźniej przy trzeciej próbie. Czy takie rozwiązanie jest prawidłowe:

1		1		1		1
	•		•		=
10		9		8		720

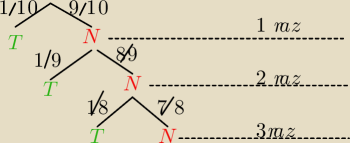
ford: nie bardzo

	1		9		1		9		8		1		1		1		1
P =		+		*		+		*		*		=		+		+		=
	10		10		9		10		9		8		10		10		10

	3
	10