Asymptoty wykresu f(x) rox: Wyznacz asymptoty pionowe wykresu funkcji f. f(x)=x²+5/x²+2x

iteRacj@: zapisz wzór funkcji w postaci ułamka lub chociaż z nawiasami

rox: / oznacza kreskę Ulamkowa, to co po prawej to licznik a po lewej mianownik, nie ma żadnych nawiasow

rox: Przepraszam.. To co po lewej licznik a po prawej mianownik

iteRacj@: u Ciebie nie ma nawiasów i dlatego nie wiadomo

	x2+5
czy f(x)=(x2+5)/(x2+2x)=
	x2+2x

	5
czy f(x)=x2+		+2x
	x2

rox: To pierwsze

iteRacj@: najpierw wyznacz dziedzinę, będziesz wiedzieć, gdzie szukac asymptot pionowych

rox: Wyszło − 2 i 0. Już zrobiłam zadanie ale mam pytanie czy dla zera liczyć z lewej i prawej strony?

iteRacj@: i prawo− i lewostronną dla −2 i dla 0

rox: Okej czyli jak wyjdzie parabola która przecina dwa punkty to robię lewo i prawo stronna a jak np będę miała x0 =1 to nie liczę dwóch stron? Tylko wtedy będzie limx→1=[1/0+]? (ewentualnie 0−). Wnioskuję tak z zeszytu ale nie jestem pewna

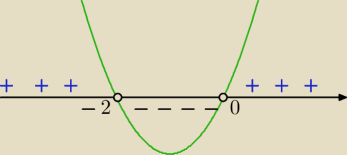
iteRacj@: w mianowniku masz funkcję kwadratową g(x)=x²+2x=x(x+2) granicę prawo− i lewostronną liczysz dlatego, że funkcja na inne wartości (raz dodatnie, a raz ujemne) gdy → −2⁻ i gdy → −2⁺ tak samo dla zera

rox: Aha czyli jak parabola będzie przecinac os x w jednym punkcie to co?

rox: Liczę dla + tylko?

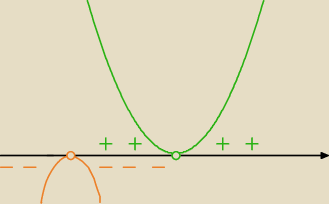
iteRacj@: wtedy granica prawostronna i lewostronna w tym punkcie będą równe jeśli masz wątpliwości, to licz osobno granice jednostronne albo x→ −2 ale nie możesz wybierać tylko jednej jednostronnej, jeśli do określenia przebiegu zmienności funkcji potrzebna jest granica w punkcie a czyli gdy D=R−{a}