Równania różniczkowe asas: Napisać równanie linii przechodzącej przez punkt (2,3) o takiej własności, że każdy odcinek stcznej do linii zawartej między osiami układu jest dzielony na połowy przez punkt stycznośćy POwiem tak, zupełnie nie rozumiem tej treści może ktoś to rozjaśnić ?

asas: Powinno być zawarty zamiast zawartej*

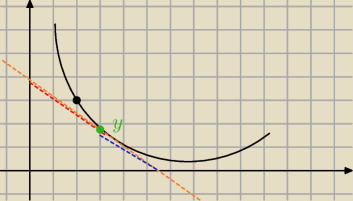
Pytający: Niezbyt piękny rysunek, ale powinien zobrazować: Dla każdej stycznej (pomarańczowa) do wykresu (czarny), czerwony fragment stycznej (od przecięcia z OY do punktu styczności) powinien być równy fragmentowi niebieskiemu (od przecięcia z OX do punktu styczności).

asas: okej, ale jak mam to sobie wyprowadzić?

asas: ...

Basia: prosta, która przecina osie w punktach A(c,0) i B(0,d)

	d
ma równanie y = −		*x + d
	c

	c		d
linia, której równanie trzba napisać musi przechodzić przez punkt (		;		)
	2		2

f(c/2) = d/2 f'(c/2) = −(d/c) podstawiamy

	c		d
x=		y=
	2		2

c=2x d=2y i mamy y = f(x)

	2y		y		f(x)
f'(x) = −		= −		= −
	2x		x		x

f(x) = −x*f'(x)

f'(x)		1
	= −
f(x)		x

	y'		1
∫		dy = −∫		dx + C
	y		x

	1
ln|y| =		+C
	x2

|y| = e^(1/x2)+C y = +e^(1/x2)+C lub y = −e^(1/x2)+C z drugiego będzie sprzeczność bo nie może być 3 = −e^(1/4)+C < 0 czyli tylko y = e^(1/x2)+C 3 = e^(1/4)+C

	1
ln3 =		+C
	4

	1
C = −		+ln3
	4

y=f(x) = e^{(1/x2)−(1/4)+ln3} = 3*e^(4−x2)/x2 mogłam się gdzieś pomylić w rachunkach

Basia: o rany błąd, okropny; wrr.............. dobrze jest do wiersza

	y'		1
∫		dy = −∫		dx
	y		x

potem powinno być ln|y| = −ln|x|+C |y| = e^−ln|x|+C y = ±e^−ln|x|+C 3 = −e^−ln(2)+C < 0 sprzecznośc czyli tylko 3 = e^−ln(2)+C ln3 = −ln2+C C = ln3+ln2 czyli y = e^{−ln|x|+ln3+ln2} = e^ln(6/|x|)