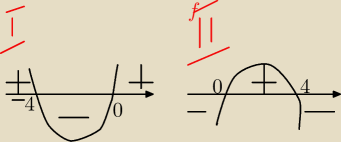pochodna hmm: Narysuj wykres funkcji f i wyznacz jej ekstrema. W których punktach funkcja ta nie ma pochodnej?

	|x2−x−2|
c) f(x)=
	x2

Blee: x²−x−2 = (x−2)(x+1) pochodnej (zapewne) nie będzie w miejscu w którym zacznie 'działać' moduł (czyli gdy licznik = 0)

hmm: Rozbijam to na 2 przypadki, i wychodzi mi że zarówno w przedziałach (−∞,−1) jak i (−1,0) jest malejąca, a powinno być najpierw malejąca, potem rosnąca i wyszłoby ekstremum

Blee: Pokaz obliczenia

hmm:

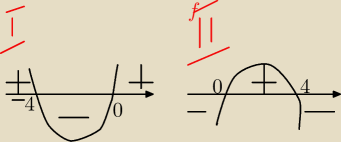
	|(x+1)(x−2)|
f(x)=		x≠0
	x2

I. x∊(−∞,−1>u<2,+∞)

	x2−x−2
f(x)=
	x2

	(2x−1)x2−2x(x2−x−2)		x+4
f'(x)=		=
	x4		x3

f'(x)=0 ⇔ x=−4 (narysowany wykres) −4 to maksimum II. x∊(−1,2)

	−x2+x+2
f(x)=
	x2

	(−2x+1)x2−2x(−x2+x+2)		−x−4
f'(x)=		=
	x4		x3

f'(x)=0⇔x=4 (narysowany wykres) 4 to maksimum, ale nie należy do dziedziny No i tu i z tych wykresów wychodzi że w I i II przypadku funkcja maleje w x∊(−4,−1) (I przypadek) i w x ∊(−1,0) (II przypadek)

hmm: ? :+(