:) poziomka: Zbadaj liczbę rozwiązań równania w zależności od wartości parametru k (k∊R): −x²+2|x|=k²−2

DM: Ja bym podszedł do tego tak: Rozważamy dwa przypadki dla x ≥ 0 oraz x < 0 i rysujemy wykresy − jeden po lewej stronie osi OY (x<0) drugi po prawej (x ≥ 0) i potem odczytujemy z wykresu i wyznaczamy z powstałych nierówności odpowiednie k.

poziomka: mam problem z odczytaniem rozwiązań właśnie

DM: a wykres masz narysowany?

poziomka: mam

Ha ha ha: Wystarczy zbadać znak Δ

DM: to przyłóż linijke do wykresu równolegle do osi OX i jedziesz od góry do dołu (albo na odwrót jak wolisz) i sprawdzasz w których miejscach przecina wykres i ile razy np. dla masz 4 rozwiązania w dla wartości (0,1) i potem rozwiązujesz nierówność 0 < k² − 2 < 1 i ten zakres 'k' jaki z tego wyszedł piszesz, że dla takich k − funkcja ma 4 rozwiązania itd. potem 0 rozwiązań 1, 2, 3 itd

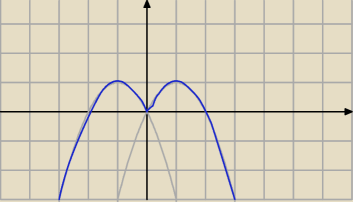
Blee: taki masz wykres k² − 2 = 1 −> k² = 3 −> k = +/−√3 (wtedy mamy 2 rozwiązania) k² − 2 ∊ (0;1) −> k² ∊ (2 ; 3) −> k ∊ (−√3 ; −√2) u (√2 ; √3) (wtedy mamy 4 rozwiązania) k² − 2 = 0 −> k = +/− √2 (wtedy mamy 3 rozwiązania) k² − 2 < 0 −> k² < 2 −> k ∊ (−√2 ; √2) (wtedy mamy 2 rozwiązania

DM: "Ha ha ha" − Jak się da prościej to chętnie się dokształce

poziomka: Dziękuje ślicznie!

LELONSTG: FUCK YEAAA

Krzysiek60: policz delte