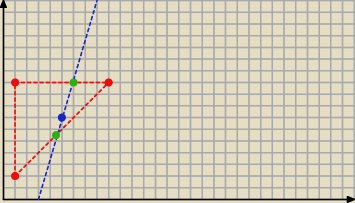
Jak rozpocząć zadanie optymalizacyjne? Adam: Dany jest trójkąt abc gdzie a(1,2) b (1,10) c(9,10). przez punkt d(5,7) przeprowadzono prostą o współczynniku kierunkowym dodatnim, która przecina boki AC i BC w punktach E i F. Wyznacz współrzędne punktów E i F dla których pole czworokąta AEFB jest największe Nie mam pojęcia jak zacząć, może ktoś pomóc?

Blee: zacznij od ... rysunku

Blee: Mam nadzieję, że pomogłem

Adam: heh, żarty żarciki ale rozwiązać by się przydało

Blee:

Adam: W pytaniu jak zacząc chodziło mi bardziej o to jak wyprowadzić wzór funkcji.

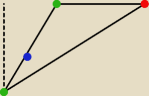
Blee: y= ax+b <−−− wzór funkcji wiemy, że D(5,7) należy do tejże funkcji, więc: 7 = 5a+b −> b = 7−5a <−−− zależność pomiędzy współczynnikami (pamiętamy o warunku: a>0) Teraz. Kiedy ów czworokąt będzie miał największe pole? Wtedy gdy trójkąt EFC będzie miał najmniejsze pole (logiczne).

	|10 − YF| * |9 − XE|
PEFC =		gdzie YF = współrzędna 'y' punktu F ; analogicznie
	2

X_E jak wiemy, tylko JEDNĄ prostą można poprowadzić przez dwa (ustalone) punkty. Więc, jeden z punktów (E lub F) traktujesz jako zmienną (a raczej jego współrzędną), a drugi punkt będzie już zależny od tego pierwszego (a raczej współrzędna drugiego). Masz równanie kwadratowe, parabola i po sprawie

Adam: Zrobiłem wg poleceń i delta mi się nie pierwiastkuje

Blee: to pokaż swoje obliczenia

Adam: E i F= (x, ax+7−5a) |10−ax+7−5a| * |9−x| P= −−−−−−−−−−−−−−−−−−−−−−−−− 2 ax²−x(3+4a)−45a+27=0 delta = 196a²+132a+9 delta a = 10368