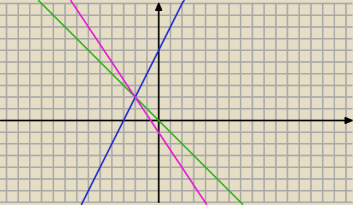
Równania prostych Pingwin4: Uzasadnij, że proste o równaniach 6x+4y+5=0, 2x−y+6=0, x+y=0 przecinają się w jednym punkcie. Najpierw obliczylabym punkt wspolny dla dwpch pierwszych anastwpnie ssprawdziła czy pasuje do trzeciego rownnaia, ale czy to dobra metoda? Poza tym chuba robie gdzies blad bo punkt nie pokrywa mi sie z ostatnim wzorem

Pingwin4: 6x+4y+4=0*

aniabb:

aniabb: metoda dobra

Pingwin4: Jak można do tego dojść? Dobrze myślałam?

aniabb: tak, metoda dobra .. może jakiś błąd rachunkowy..wpisz obliczenia

jc: 6(6x+4y+4)−4(2x−y+6)=28(x+y) Wniosek, jeśli jakiś punkt leży równocześnie na pierwszej i drugiej prostej, to leży również na trzeciej prostej. (mnożyłem tak, aby pozbyć się ostatnich składników)

Pingwin4: Bardzo dziękuję, już znalazłam błąd w rachunkach