Styczne do okręgu Grzechu: dany jest okrąg o równaniu x²+y²−10x−8y+21=0 Napisz równanie stycznych do tego okręgu w jego punktach przecięcia z osia OX. Wyszło mi punkty (3,0) i (7,0). Próbowałem policzyć dalej wykorzystując wzór na odległość od środka okręgu, ale wychodzą mi głupoty, mógłby ktoś skończyć do końca to zadanie?

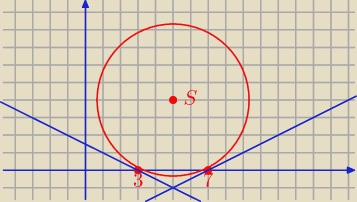
Janek191: ( x − 5)² − 25 + ( y − 4)² − 16 + 21 = 0 ( x − 5)² + ( y − 4)² = 20 S = ( 5, 4) r = 2√5 y = 0 ( x − 5)² = 4 x − 5 = 2 lub x − 5 = − 2 x = 7 lub x = 3 A = ( 3, 0) B = ( 7, 0) S = ( 5, 4) a = 2 y = −0,5 x + b 0 = −1,5 + b b = 1,5 y = − 0,5 x + 1,5 ============== oraz y = 0,5 x − 3,5 =============

Janek191: Piszemy równanie prostej AS a później prostej prostopadłej do pr AS przechodzącej przez A. Analogicznie − równanie pr BS i prostej do niej prostopadłej przechodzącej przez B.

Grzechu: Skąd te (x−5)² = 4 ?

Janek191: Dla y = 0 równanie okręgu (x − 5)² + ( y − 4)² = 20 przyjmuje postać (x − 5)² = 4

Grzechu: a dobra dzięki wielkie

aniabb: równanie stycznej w punkcie P(x_p;y_p) należącym do okręgu o środku S(a;b) i promieniu r (x−a)(x_p−a) + (y−b)(y_p−b)=r² czyli za jedno x i y w równaniu okręgu wstawiasz współrzędne punktu fajny wzorek, ale mało kiedy punkt należy do okręgu, więc nieczęsto ma zastosowanie