Zadanie optymalizacyjne smutna_buzia: Dana jest funkcja określona równaniem f(x) = −x² + 9. W punkcie P o dodatniej odciętej poprowadzono styczną do wykresu tej funkcji. Oblicz odciętą punktu P tak, aby pole trójkąta ograniczonego tą styczną i dodatnimi półosiami współrzędnych było najmniejsze. Oblicz to najmniejsze pole.

piotr: Styczna do wykresu f(x) w (x_P; f(x_P)): y = f'(x_P)(x − x_P)+ f(x_P) = −2x_P(x − x_P) − x_P² + 9 Punkty przecięcia się stycznej z osiami: OX: −2x_P(x − x_P) − x_P² + 9 = 0 ⇒

	xP2 + 9
x =
	2 xP

OY: y = −2x_P(0 − x_P) − x_P² + 9 = x_P² + 9 Pole:

	1		xP2 + 9
A(xp) =		(		)(xP2 + 9); zał.: xp > 0
	2		2 xP

	3 (xp2−3) (xp2+9)
A'(xp) =
	4 xp2

A'(x_p) = 0 ⇒ (x_p = −√3 ∨ x_p = √3 ) ∧ x_p > 0 ⇒ x_p = √3 A_min(√3) = 12√3

smutna_buzia: Dzięki

piotr: styczna y = 6 − 2 √3 (−√3 + x)

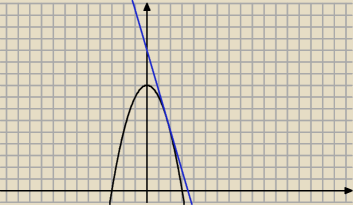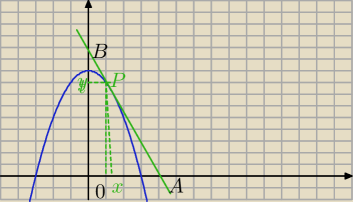PW: Styczna w punkcie P wyznacza na dodatnich półosiach wierzchołki A i B trójkąta BOA. Jeżeli styczna ma równanie y=ax+b, to współczynnik kierunkowy a jest równy pochodnej w punkcie x_P funkcji f(x)=−x²+9, czyli a=−2x_P, równanie stycznej ma postać y=−2x_Px+b. Styczna przechodzi przez punkt (x_P,f(x_P)), a więc −(x_P)²+9=−2x_Px_P+b (1) b=x_P²+9. Ostatecznie styczna ma równanie y=−2x_Px+x_P²+9. Punkt przecięcia stycznej z osią OY to b, zaś przecięcia z osią OX to taki punkt x_A, dla którego 0=−2x_Px_A+x_P²+9 2x_Px_A=x_P²+9

	xP2+9
(2) xA=		.
	2xP

Pole S trójkąta BOA jest funkcją zmiennej x_P (mnożymy przyprostokątne (1) i (2)):

	1		xP2+9
S(xP)=		(xP2+9)		, xP>0
	2		2xP

	(xP2+9)2
S(xP)=
	4xP

Dla wygody zapiszmy ją w postaci

	(x2+9)2
S(x)=		, x>0
	4x

	x4+18x2+81
S(x)=
	4x

	1		81
(3) S(x)=		(x3+18x+		)
	4		x

	1		81
S'(x)=		(3x2+18−		)
	4		x2

	81		−6+12
S'(x)=0 ⇔ (3x2+18−		)=0 ⇔ 3x4+18x2−81=0 ⇔ x4+6x2−27=0 ⇔ x2=		⇔ x2=3 ⇔
	x2		2

⇔ x=√3 (uwzględniamy warunek x>0). Tu powinno być uzasadnienie, dlaczego S(√3)= S_min. Podstawiamy do (3):

	1		81
Smin=S(√3)=		(3√3+18√3+		)=U{1}{4](21√3+27√3)=12√3.
	4		√3

PW: Przepraszam, piotrze, ale nie widziałem Twojego rozwiązania