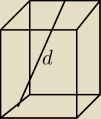
Optymalizacja, graniastosłupy szyk: Odcinek łączący środki dwóch skośnych krawędzi podstaw graniastosłupa prawidłowego czworokątnego ma długość d. Jaką wysokość powinien mieć ten graniastosłup, aby pole jego powierzchni bocznej było maksymalne?

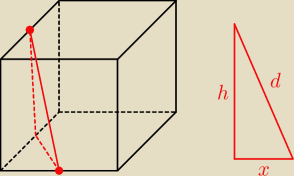Blee: czyli masz taki trójkąt prostokątny,

	√2
gdzie x = √a2/2 =		a gdzie a −−− długość krawędzi podstawy
	2

aby wyznaczyć jaką powinna być wysokość tegoż graniatosłupa prawidłowe, konieczna jest także informacja co do 'a'. W podanej treści zadania brak takiej informacji (ani jakiejkolwiek informacji pomagającej wyznaczyć 'a' ), więc samo zadanie nie jest możliwe do rozwiązania.

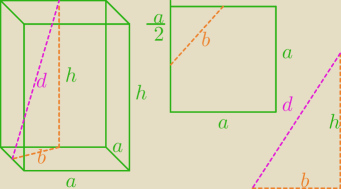iteRacj@: @Blee a czy moje rozwiązanie ma sens ? skorzystałam z tego, że to graniastosłup prawidłowy czworokątny ? P_b=4ah, 0<h<d, a>0

	a2		a2		a2
b2=		+		=
	4		4		2

a2
	=d2−h2
2

a=√2*√d²−h² P_b=4h√2*√d²−h²=4√2*√d²h²−h⁴ P(h)=4√2*√d²h²−h⁴ Funkcja P(h) przyjmuje najwiekszą wartość, gdy funkcja podpierwiastkowa przyjmuje najwiekszą wartość. Szukamy maksimum funkcji f(h)=d²h²−h⁴. f'(h)=2d²h−4h³=−2h(2h²−d²)=−2h(√2h−d)(√2h+d)

	√2
h=		d → f'(h)=0,
	2

	√2		√2
dla h<		d f'(h)>0, dla h>		d f'(h)<0
	2		2

	√2
gdy h=		d to f(x) osiąga maksimum
	2

	√2
stąd dla h=		d pole powierzchni bocznej P(h) tego graniastosłupa będzie największe.
	2

? ? ?