Wyznacz wszystkie wartości parametru m ktostaki: Wyznacz wszystkie wartości parametru m, dla których równanie | | x − 2 | − 12 | = m³ + m² ma dokładnie cztery rozwiązania

aniabb: 0<m³+m²<12

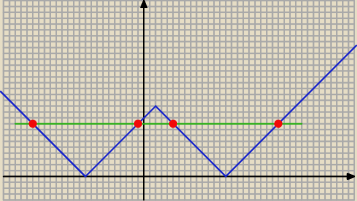
DM: Chyba najłatwiej będzie to odczytać z wykresu: 1) Rysujemy wykres funkcji liniowej f(x) = x−2 2) Odbijamy dolną część względem osi OX 3) Przesuwamy o 12 jednostek w dół 4) Powtórz punkt 2. i teraz widzimy, że m³ + m² ∊ <0, 12> czyli rozwiązujemy nierówność: 0 ≤ m³ + m² ≤ 12 Rozbijamy na dwa przypadki i łączymy spójnikiem logicznym "and": a) 0 ≤ m²(m+1) and b) m³ + m² − 12 ≤ 0 a) tu możemy narysować wykres wielomianu, który przecina oś OX w punktach {0, −1} przy czym zero to pierwiastek podwójny, rysujemy z prawej od góry b) możemy wykorzystać twierdzenie Bezout: m = 2 spełnia nierówność więc: (m−2)(m² + 3m + 6) drugi nawias nie ma rozwiązań rzeczywistych więc wykres przecina oś OX tylko w punkcie m = 2, rysujemy od prawej z góry mamy więc: m ∊ <−1, +∞) / {0} and m ∊ (−∞, 2) czyli: <−1; 2) / {0}

DM: POPRAWKA: przedziały mają być otwarte tak jak napisała aniabb, czyli {−1} odpada

PW: ||x−2|−12|=m³+m² nie ma rozwiązań, gdy prawa strona jest liczbą ujemną, zakładamy więc m³+m²≥0. Widać również, że dla m=0 badane równanie ma tylko 2 rozwiązania, w dalszym ciągu zakładamy więc m³+m²>0 m²(m+1)>0 (1) m>−1 ∧ m≠0. Dla takich m równanie jest równoważne alternatywie |x−2|−12=m³+m² ∨ |x−2|−12=−(m³+m²) (2) |x−2|=m³+m²+12 ∨ |x−2|=−m³−m²+12. Z uwagi na założenie (1) pierwsze z równań (2) ma dwa rozwiązania. Aby drugie z równań (2) też miało dwa rozwiązania, prawa strona musi być liczbą dodatnią, to znaczy −m³−m²+12>0 m³+m²−12<0 (m−2)(m²+3m+6)<0 Drugi czynnik jest zawsze dodatni, musi być więc (3) m<2. Nierówności (1) i (3) są jednocześnie spełnione, gdy m>−1 ∧ m≠0 ∧ m<2 ⇔ m∊(−1,2)\{0}. Wniosek. Badne równanie jest równoważne alternatywie równań (2), z których pierwsze ma dwa rozwiązania przy założeniu (1), zaś drugie też ma dwa rozwiazania przy założeniu (1) i (3). Rozwiązania obu równań (2) są w sposób oczywisty różnymi czterema liczbami. Odpowiedź. Równanie ma 4 rozwiązania dla m∊(−1,2)\{0}.