trójkąt mati: W trójkacie równoramiennym ABC podstawa AB=4 wysokość CD=6 Okrąg którego średnicą jest bok AC przecina bok BC w punkcie M Oblicz pole trójkąta DBM

Mila: JUtro Dobranoc

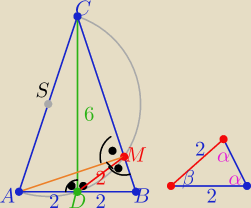
Eta: 1/ rysunek ..... 2/ trójkąty ADC i AMC i ABM są prostokątne ( dlaczego ...... 3/D jest środkiem przeciwprostokątnej ΔABM to |DM|=|AB|/2=2 zatem ΔDBM jest równoramienny o kącie β między ramionami

	1
P(DBM)=		*2*2*sinβ= 2sinβ
	2

należy wyznaczyć sinβ .... 180^o−2α to sinβ= sin2α= 2sinα*cosα 4/ w ΔDBC tgα= 3 to sinα= 6/√36+4= 3/√10 to cosα= 1/√10 zatem P(DBM)= 2*2*(3/√10)*(1/√10) = 6/5=1,2 P(DBM)= 1,2 ============ To jeden ze sposobów Może Mila poda inny sposób

Eta: 2 sposób łatwiejszy skoro ΔDBM jest równoramienny i ΔABC też równoramienny o kątach α przy podstawach więc są trójkątami podobnymi |BC|=√6²+2²=2√10

	2√10
w skali k=		= √10
	2

to pola są w skali k²=10 zatem P(ABC)= 12 to P(DBM) = 12/10= 1,2